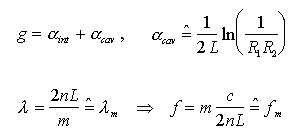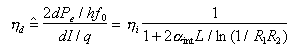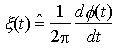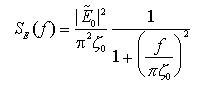|
|
|
Tecnologie di Base
e Applicazioni |
Introduzione
Nel campo delle telecomunicazioni le sorgenti ottiche utilizzate per la trasmissione di segnali ottici sono principalmente dispositivi a semiconduttore. Tali dispositivi sono di due tipi: diodi emettitori di luce (LED, Light Emitting Diode) e diodi ad amplificazione luminosa per emissione stimolata di radiazione (LASER, Light Amplification by Stimulated Emission of Radiation) e si basano su fenomeni di emissione della radiazione elettromagnetica che è possibile descrivere mediante principi elementari di meccanica quantistica. Vediamo brevemente questi principi nell'ipotesi di considerare la radiazione elettromagnetica secondo la teoria quantistica corpuscolare.
L'interazione della radiazione elettromagnetica con la materia avviene mediante tre fenomeni fondamentali: assorbimento, emissione spontanea ed emissione stimolata, tutti relativi all'emissione di un fotone da parte di un atomo. In particolare quando un fotone a frequenza f0 e, quindi, energia h*f0 interagisce con un atomo, esso può essere assorbito provocando la transizione di un elettrone dal livello E1 al livello E2 > E1 (E2 = E1 + h*f0). Gli elettroni eccitati, a partire da questo stato, possono tornare allo stato originario attraverso l'emissione spontanea di un fotone con energia h*f0 oppure, se un fotone interagisce con un atomo con un elettrone sul livello E2, si può avere emissione stimolata di un ulteriore fotone con energia h*f0, che accompagna il fotone originario e la transizione dell'atomo sul livello E1.

Fig. 2.1 - Fenomeni di interazione radiazione/materia
La caratteristica principale dell'emissione stimolata è che il fotone secondario ha la stessa energia e la stessa direzione (quantità di moto) del fotone primario. Al campo elettromagnetico, dovuto ai fotoni primari, si aggiungono i contributi dei fotoni secondari che, per quanto detto, possono considerarsi in fase con i fotoni primari dando luogo all'emissione coerente, caratterizzata da un'unica frequenza di emissione. L'emissione stimolata viene amplificata e convogliata all'esterno, nelle sorgenti LASER, ottenendo un alto grado di coerenza temporale (teoricamente) ovvero un raggio monocromatico. I fotoni che si creano per emissione spontanea hanno direzioni di propagazione aleatorie e si ricombinano con relazioni arbitrarie fornendo una emissione incoerente ovvero caratterizzata da uno spettro di emissione ampio (tipico del LED).
Un'analisi dettagliata dei fenomeni accennati porta alla conclusione che i tassi 4 (rate) di emissione sono dati da
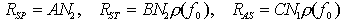
ove N1 ed N2 sono le densità degli atomi nello stato fondamentale E1 ed eccitato E2, rispettivamente, e 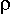 (f0) è la densità spettrale di potenza della radiazione che investe il materiale, valutata alla frequenza f0. (f0) è la densità spettrale di potenza della radiazione che investe il materiale, valutata alla frequenza f0.
All'equilibrio termico N1 ed N2 sono regolate dalla distribuzione di Boltzmann, ovvero
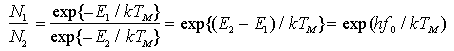
ove T è la temperatura assoluta e k è la costante di Boltzmann 5. Alle frequenze tipiche delle trasmissioni ottiche e per temperatura ambiente si ha che h*f0 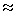 1 eV e k*T 1 eV e k*T 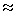 0.03 eV cosicché N1 >> N2, cioè il livello base è molto più popolato del livello eccitato così come è lecito aspettarsi. Poichè all'equilibrio termico, N1 ed N2 sono stazionari, i tassi di assorbimento e di emissione totale devono coincidere 0.03 eV cosicché N1 >> N2, cioè il livello base è molto più popolato del livello eccitato così come è lecito aspettarsi. Poichè all'equilibrio termico, N1 ed N2 sono stazionari, i tassi di assorbimento e di emissione totale devono coincidere
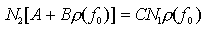
da cui si ottiene
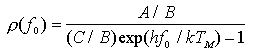 . .
Poichè la legge di Planck del corpo nero prevede una radiazione all'equilibrio termico pari a
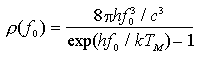
combinando quest'ultima con le precedenti relazioni si ottengono le relazioni di Einstein
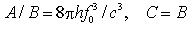
e, di conseguenza, anche i tassi di emissione finali
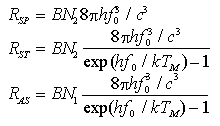
ove B dipende dal materiale utilizzato.
Dalle relazioni precedenti si osserva che RSP >> RST, RAS per le lunghezze d'onda dell'infrarosso vicino all'equilibrio termico e per qualunque temperatura ragionevole. Per ottenere una emissione stimolata è, allora, necessario operare lontano dall'equilibrio termico. Inoltre per avere una considerevole emissione stimolata tale da non temere l'assorbimento, si deve avere che N2 >> N1 ovvero si deve verificare il fenomeno dell'inversione di popolazione.
2.1 - Emissione Luminosa nei Semiconduttori
2.1.1 - Il Diodo Emettitore di Luce
Tra i materiali più adatti da impiegare come emettitori di radiazione luminosa alle lunghezze d'onda di interesse (infrarosso vicino) vi sono i semiconduttori. In questi materiali si ritrova la struttura a due livelli: al livello E2 corrisponde la Ec della banda di conduzione mentre ad E1 corrisponde la Ev della banda di valenza. Abbiamo visto che f0, ovvero  0, è determinata dalla cosiddetta energia di gap Eg = Ec - Ev = h*f0 caratteristica del particolare materiale (ad esempio per il Silicio Eg = 1.1 eV mentre per il Germanio Eg = 1.42 eV, cui corrispondono, rispettivamente, lunghezze d'onda pari a 1.13 0, è determinata dalla cosiddetta energia di gap Eg = Ec - Ev = h*f0 caratteristica del particolare materiale (ad esempio per il Silicio Eg = 1.1 eV mentre per il Germanio Eg = 1.42 eV, cui corrispondono, rispettivamente, lunghezze d'onda pari a 1.13  m e 0.87 m e 0.87  m). m).
Ogni volta che, nel semiconduttore, un elettrone eccitato nella banda di conduzione ritorna nella banda di valenza (ricombinazione elettrone/lacuna) si ha l'emissione di un fotone alla lunghezza d'onda  0. Sfortunatamente a temperatura ambiente la concentrazione di elettroni eccitati è piccola per avere una emissione significativa, anche se il semiconduttore è fortemente drogato ed è, quindi, necessario ricorrere ad una sorgente esterna per aumentare il numero di elettroni eccitati. Il modo più semplice per raggiungere questo scopo è realizzare una giunzione p-n polarizzata direttamente iniettando, così, un elevato numero di elettroni nella zona di svuotamento (zona attiva). La ricombinazione di tali cariche può verificarsi in due modi: ricombinazione radiativa e non radiativa. Nel primo tipo la ricombinazione dà luogo all'emissione di un fotone contribuendo all'intensità della radiazione prodotta; nel secondo tipo la ricombinazione avviene in modo tale che l'energia di gap non viene ceduta come fotone ma trasferita ad altri portatori come energia cinetica o dissipata in fononi di vibrazione del reticolo oppure, ancora, assorbita da impurità del materiale. È evidente che l'intensità della radiazione in corrispondenza di una data corrente I di polarizzazione, dato che il meccanismo di ricombinazione è il medesimo per tutti i materiali, dipende dalla probabilità che all'interno del semiconduttore si verifichino delle ricombinazioni non radiative; poichè il silicio presenta una elevata probabilità di ricombinazione non radiativa, negli anni '60 il materiale che ha permesso la costruzione dei primi dispositivi optoelettronici è stato l'arseniuro di gallio (GaAs) che presenta una bassa probabilità di questo tipo. 0. Sfortunatamente a temperatura ambiente la concentrazione di elettroni eccitati è piccola per avere una emissione significativa, anche se il semiconduttore è fortemente drogato ed è, quindi, necessario ricorrere ad una sorgente esterna per aumentare il numero di elettroni eccitati. Il modo più semplice per raggiungere questo scopo è realizzare una giunzione p-n polarizzata direttamente iniettando, così, un elevato numero di elettroni nella zona di svuotamento (zona attiva). La ricombinazione di tali cariche può verificarsi in due modi: ricombinazione radiativa e non radiativa. Nel primo tipo la ricombinazione dà luogo all'emissione di un fotone contribuendo all'intensità della radiazione prodotta; nel secondo tipo la ricombinazione avviene in modo tale che l'energia di gap non viene ceduta come fotone ma trasferita ad altri portatori come energia cinetica o dissipata in fononi di vibrazione del reticolo oppure, ancora, assorbita da impurità del materiale. È evidente che l'intensità della radiazione in corrispondenza di una data corrente I di polarizzazione, dato che il meccanismo di ricombinazione è il medesimo per tutti i materiali, dipende dalla probabilità che all'interno del semiconduttore si verifichino delle ricombinazioni non radiative; poichè il silicio presenta una elevata probabilità di ricombinazione non radiativa, negli anni '60 il materiale che ha permesso la costruzione dei primi dispositivi optoelettronici è stato l'arseniuro di gallio (GaAs) che presenta una bassa probabilità di questo tipo.
L'attitudine di un semiconduttore alla ricombinazione non radiativa rispetto ad un altro può spiegarsi studiando più a fondo la modalità di transizione dallo stato Ec allo stato Ev. Infatti, oltre alla già vista conservazione dell'energia Eg = Ev + h*f0, la transizione richiede la conservazione della quantità di moto (p = h*f0/c, indicata come impulso) dallo stato eccitato p2 allo stato base p1. Essendo la quantità di moto del fotone molto minore di p1, la quantità di moto dei portatori di carica non viene alterata dalla sua emissione. Di conseguenza, i semiconduttori vengono distinti (figura seguente) in a gap diretto (GaAs) ed a gap indiretto (Ge, Si). Nel GaAs la banda di valenza e quella di conduzione sono direttamente affacciate (massimo di Ev e minimo di Ec) e, quindi, la transizione può avvenire in accordo ai due principi di conservazione con facilità. Nel Si, invece, la transizione non può avvenire direttamente in quanto il fotone non consente il salto di impulso ed è necessario l'intervento di un'altra particella con energia piccola ma grande quantità di moto (fonone).

Fig. 2.2 - Diagrammi di stato (E-p) di semiconduttori a gap diretto (a) ed indiretto (b).
Nei semiconduttori a gap indiretto è, quindi, meno probabile che avvenga la transizione. È chiaro, allora, perchè un LED debba essere costituito di semiconduttore a gap diretto ed essere polarizzato direttamente.
Per caratterizzare i tipi di LED in commercio si introduce un parametro di efficienza. Introducendo i tassi di ricombinazione radiativa, Rr, e non radiativa, Rnr, si definisce efficienza quantistica interna la quantità
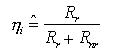
ove Rr = RSP + RST 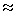 RSP. RSP. 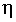 i sarà, ovviamente, massimo quando Rr è molto maggiore di Rnr; valori tipici di i sarà, ovviamente, massimo quando Rr è molto maggiore di Rnr; valori tipici di 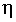 i per GaAs ed InP (fosfuro d'indio) sono intorno a 0.5. Se q è la carica dell'elettrone ed I la corrente che attraversa il dispositivo, allora la potenza luminosa generata all'interno della zona attiva è i per GaAs ed InP (fosfuro d'indio) sono intorno a 0.5. Se q è la carica dell'elettrone ed I la corrente che attraversa il dispositivo, allora la potenza luminosa generata all'interno della zona attiva è
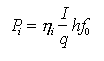 . .
Pi può superare facilmente i 10 mW ma la potenza effettivamente presente all'esterno del dispositivo è limitata dall'assorbimento della radiazione nel tratto tra zona attiva e superfice esterna e da fenomeni di riflessione all'interfaccia semiconduttore/aria. Poichè l'indice di rifrazione di un semiconduttore è elevato (> 3), l'angolo critico è piuttosto piccolo(< 20 °) e, quindi, per tenere conto di una riflessione anche rilevante, si deve introdurre un nuovo parametro (rendimento esterno 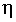 ext) che viene inglobato nella efficienza quantistica totale ext) che viene inglobato nella efficienza quantistica totale
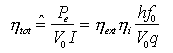
ove Pe è la potenza ottica disponibile esternamente, V0 è la tensione applicata sul LED stesso (V*I è la potenza elettrica dissipata sul dispositivo). Si introduce, poi, un ulteriore parametro, detto responsivity, per legare la potenza ottica disponibile alla corrente di pilotaggio I:
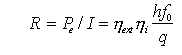 . .
In questa semplice analisi si è trascurata la dipendenza di  i dalla corrente I e dalla temperatura T. Sperimentalmente si trova l'andamento riportato nella figura seguente. i dalla corrente I e dalla temperatura T. Sperimentalmente si trova l'andamento riportato nella figura seguente.

Fig. 2.3 - Caratteristica esterna P/I di un LED ad 1.3  m m
Non va dimenticato, inoltre, che la faccia emittente del LED deve, poi, essere accoppiata alla fibra ottica ed in particolare, si dimostra che per una fibra con apertura numerica NA l'efficienza di accoppiamento è pari a (NA)2, nel caso in cui si possa considerare la superficie piana del LED come una sorgente Lambertiana 6.
2.1.2 - Tecniche di Fabbricazione e Larghezza Spettrale
Tra i fattori positivi per i quali i LED vengono impiegati nei sistemi di trasmissione ottica vi sono:
- semplicità di fabbricazione;
- basso costo;
- alta affidabilità;
- buona linearità della caratteristica corrente/potenza;
- semplicità dei circuiti elettrici di pilotaggio;
- relativa insensibilità a variazioni della temperatura;
mentre, per contro, tra i principali inconvenienti vi sono:
- bassa potenza lanciata in fibra (decine di
 W); W);
- largo spettro di emissione (
 12-17 THz); 12-17 THz);
- stretta banda di modulazione (
 100 MHz). 100 MHz).
Per migliorare il rendimento dei LED e facilitare l'accoppiamento alla fibra ottica vengono adottati alcuni accorgimenti nella fabbricazione dei medesimi. Una semplice giunzione p-n (omogiunzione), in cui si ha una variazione brusca del tipo di drogaggio nel medesimo materiale, è caratterizzata da una regione di svuotamento ampia consentendo, così, la ricombinazione dei portatori iniettati dalla corrente diretta in una vasta regione, limitando la densità di carica. Si rende necessario confinare i portatori in una zona più piccola per aumentare la densità di carica e, quindi, il flusso ottico, attraverso la doppia eterogiunzione (DH, Double Hetero-junction), nella quale una zona di semiconduttore eterogeneo viene inserita tra gli starti omogenei p ed n preesistenti.
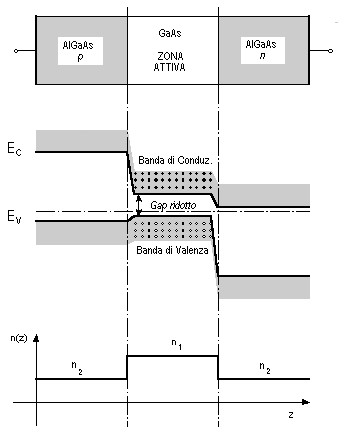
Fig. 2.4 - Confinamento dei portatori e dell'emissione in un LED ad eterostruttura.
Lo strato eterogeneo può essere drogato o intrinseco ma, in ogni caso, il suo scopo è quello di confinare al proprio interno i portatori iniettati mediante la corrente di conduzione. Il confinamento è dovuto alla discontinuità nei livelli energetici dei materiali (in particolare per la diversa energia di gap Eg) scelti appositamente con la medesima struttura cristallina e differenti Eg, tipicamente GaAs e AlGaAs. Generalmente la Eg dello strato attivo (eterogeneo) è minore della Eg dello strato di mantello (semiconduttore circostante) per cui, come si vede nella figura precedente, l'indice di rifrazione dello strato attivo è maggiore dell'indice del mantello. Lo strato attivo si comporta come una guida d'onda ottica rettangolare confinando al suo interno sia i portatori elettrici sia i fotoni generati per emissione spontanea durante la ricombinazione dei portatori stessi. Le due principali configurazioni per i LED per telecomunicazioni sono mostrate nelle figure seguenti e sono indicate come diodo ad emissione superficiale (o di Burrus) e diodo ad emissione laterale con geometria a striscia.

Fig. 2.5 - LED di Burrus a doppia eterogiunzione.

Fig. 2.6 - LED ad emissione laterale con doppia eterogiunzione.
Nel diodo di Burrus la luce è emessa ortogonalmente ad un piano parallelo alla giunzione e l'area di emissione viene ridotta alla dimensione della sezione trasversale del nucleo della fibra; quest'ultima viene accoppiata al LED con resina epossidica che tende ad aumentare l'efficienza esterna del dispositivo.
Nel diodo ad emissione laterale la luce viene confinata su una striscia parallela al piano di giunzione, consentendo una densità di iniezione dei portatori maggiore che nel diodo ad emissione superficiale. In questo diodo la luce è raccolta su di un piano perpendicolare alla giunzione evitando dispersioni attraverso la faccia opposta a quella emittente trattando la prima con un rivestimento riflettente. Anche in questo caso le proprietà di guida dei due strati di mantello consentono un buon accoppiamento alla fibra poichè la larghezza del fascio di luce risulta stretta su di un piano perpendicolare alla giunzione.
La banda dell'emissione è il fattore che maggiormente limita l'utilizzo del LED come sorgente ottica nei sistemi ad alta velocità. L'emissione spontanea, infatti, che caratterizza il funzionamento del LED, origina un segnale che non possiede quella coerenza temporale posseduta da un segnale prodotto per emissione stimolata e, analizzando il fenomeno dell'emissione spontanea, si ricava una larghezza dello spettro, indicata come Full Width Half Maximum (FWHM, ovvero la banda a -3 dB), pari a
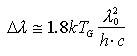 . .
Si vede subito che   aumenta con aumenta con  0, cosicché i LED con 0, cosicché i LED con  0 = 1.3 0 = 1.3  m hanno larghezza spettrale maggiore dei LED con m hanno larghezza spettrale maggiore dei LED con  0 = 0.85 0 = 0.85  m. m.
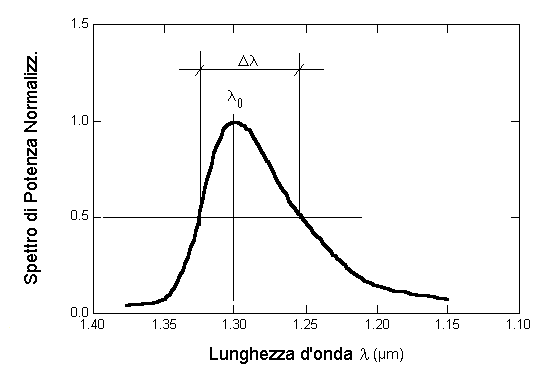
Fig. 2.7 - Spettro di emissione di un LED a 1.3  m. m.
Nella figura precedente è riportato il tipico spettro per un LED con  0 = 1.3 0 = 1.3  m, per il quale m, per il quale 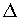  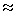 50-60 nm e, quindi, la dispersione della fibra limita molto l'uso del LED come sorgente ad alta velocità per lunghe tratte anche lavorando alla 50-60 nm e, quindi, la dispersione della fibra limita molto l'uso del LED come sorgente ad alta velocità per lunghe tratte anche lavorando alla  ZD. Un altro problema che si pone in presenza di elevate velocità di modulazione è il fenomeno dell'inerzia dei portatori che limita la velocità di risposta del LED. Infatti, maggiore è il tempo medio di ricombinazione ZD. Un altro problema che si pone in presenza di elevate velocità di modulazione è il fenomeno dell'inerzia dei portatori che limita la velocità di risposta del LED. Infatti, maggiore è il tempo medio di ricombinazione 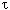 c (tempo di permanenza nello stato eccitato) e maggiore è l'inerzia del LED alla modulazione in quanto i portatori non hanno il tempo di seguire le variazioni dovute alla corrente di pilotaggio modulata. Senza entrare in ulteriori dettagli, si dimostra che, imponendo una riduzione di 3 dB sulla potenza ottica di uscita in regime sinusoidale rispetto al valore in regime continuo, la banda di modulazione Bm risulta c (tempo di permanenza nello stato eccitato) e maggiore è l'inerzia del LED alla modulazione in quanto i portatori non hanno il tempo di seguire le variazioni dovute alla corrente di pilotaggio modulata. Senza entrare in ulteriori dettagli, si dimostra che, imponendo una riduzione di 3 dB sulla potenza ottica di uscita in regime sinusoidale rispetto al valore in regime continuo, la banda di modulazione Bm risulta
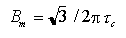
che, per valori tipici di 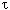 c ( c (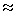 1 - 5 ns), fornisce Bm = 60 - 300 MHz. 1 - 5 ns), fornisce Bm = 60 - 300 MHz.
2.2 - LASER Fabry-Pérot ed a Semiconduttore
2.2.1 - Condizioni di funzionamento
Si è visto nelle pagine precedenti che, per ottenere una sorgente luminosa in cui è predominante il fenomeno della emissione stimolata, ovvero con elevata coerenza temporale, si devono verificare due condizioni:
- la distribuzione degli stati energetici degli atomi non deve essere relativa ad una situazione di equilibrio termico;
- si deve realizzare l'inversione della popolazione dei due livelli.
In particolare, quest'ultima condizione può ottenersi eccitando il materiale con una sorgente di energia esterna ed effettuando il cosiddetto pompaggio. Così facendo, tuttavia, si può ottenere al massimo una equipartizione e non una vera inversione della popolazione dei due livelli energetici. Per risolvere questo problema si deve ricorrere ad un sistema a più livelli; si può usare, ad esempio, un sistema a tre livelli (LASER a cristallo di rubino) in cui gli atomi vengono pompati dallo stato base E1 ad un livello E3 (instabile) più elevato del livello metastabile E2.
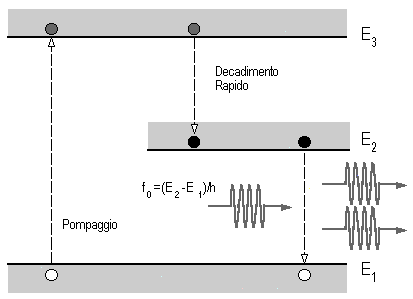
Fig. 2.8 - Sistema a tre livelli.
In E3 gli atomi restano per un tempo breve decadendo velocemente, con un decadimento non radiativo, sul livello E2 (metastabile perchè il tempo di permanenza è elevato), consentendo di avere tempo sufficiente affinchè vi sia un accumulo degli atomi su E2 tale da realizzare l'inversione di popolazione. Tra i livelli E2 ed E1 si realizza l'emissione stimolata, come già descritto per il sistema a due livelli; è necessario, tuttavia, prendere in considerazione schemi a quattro livelli (LASER a semiconduttore), almeno in alcuni casi, perchè in essi l'inversione si può ottenere più semplicemente con meno energia di pompaggio tra i due livelli intermedi.

Fig. 2.9 - Sistema LASER a quattro livelli.
In questi sistemi, infatti, si ha un livello base E0 (stabile) minore di E1 (instabile) a partire dal quale gli atomi vengono pompati direttamente su E3 (instabile): si ha, quindi, prima la transizione non radiativa da E3 ad E2 (metastabile) e poi la transizione radiativa da E2 ad E1 ed, infine, gli atomi passano rapidamente su E0 da E1.
2.2.2 - Laser a Cavità
Il LASER nasce come amplificatore di segnali ottici secondo il fenomeno dell'emissione stimolata, in quanto il mezzo sede di quest'ultimo (amplificazione ottica) si può caratterizzare dal guadagno ottico per unità di lunghezza g, il quale varia al variare della lunghezza d'onda ed è caratteristico del materiale e della modalità di pompaggio. Il LASER è, però, prevalentemente usato come sorgente luminosa, in cui viene prodotto autonomamente un segnale ad una fissata  0 e, nella terminologia delle telecomunicazioni, viene indicato come oscillatore ottico. Il modo più semplice di trasformare un amplificatore in un oscillatore è quello di reazionarlo positivamente e ciò viene fatto nel LASER confinando il segnale ottico amplificato per emissione stimolata in una porzione definita del materiale amplificatore, soddisfacendo opportune condizioni di coerenza temporale. 0 e, nella terminologia delle telecomunicazioni, viene indicato come oscillatore ottico. Il modo più semplice di trasformare un amplificatore in un oscillatore è quello di reazionarlo positivamente e ciò viene fatto nel LASER confinando il segnale ottico amplificato per emissione stimolata in una porzione definita del materiale amplificatore, soddisfacendo opportune condizioni di coerenza temporale.
Un modo per ottenere quanto detto è l'uso di una "cavità" (ottica), cioè dotare di facce riflettenti i lati contrapposti del mezzo amplificatore.

Fig. 2.10 - Schema di principio del LASER a cavità Fabry-Pérot.
Il segnale all'interno della cavità subisce riflessioni multiple e viene contestualmente amplificato in modo da autosostenere una oscillazione (onda stazionaria). Se le due facce sono parzialmente riflettenti è possibile estrarre una parte dell'emissione interna, purché la perdita di potenza non sia tale da disinnescare l'oscillazione, per accoppiarla esternamente. Quando il guadagno ottico, all'interno del materiale, bilancia esattamente le perdite interne per assorbimento e la parte di segnale trasmesso all'esterno, si ottiene la condizione di stabilità dell'oscillazione e, quindi, quando il pompaggio è sufficiente a ottenere l'inversione della popolazione, la cavità comincia ad oscillare spontaneamente ed ad autosostenersi. È intuibile che il segnale, durante le ripetute propagazioni nel materiale, deve poter mantenere la caratteristica di coerenza temporale dell'emissione stimolata, per cui l'oscillazione si può avere solo quando la distanza L tra le facce è in relazione ben precisa con la lunghezza d'onda  . .
Deriviamo le relazioni di stabilità e di frequenza dell'oscillazione dalle considerazioni seguenti. Consideriamo un'onda monocromatica che si propaga nella cavità secondo la direzione z, come nella figura precedente. Affinché l'oscillazione si autosostenga, indicando con 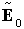 il fasore del campo elettrico per z = 0+, il fasore del campo deve trovarsi "inalterato" al punto di partenza dopo la seconda riflessione sulla faccia 1, cioè il fasore del campo elettrico per z = 0+, il fasore del campo deve trovarsi "inalterato" al punto di partenza dopo la seconda riflessione sulla faccia 1, cioè
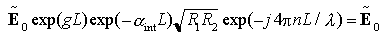
ove
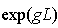 , fattore di amplificazione durante il percorso (andata e ritorno); , fattore di amplificazione durante il percorso (andata e ritorno);
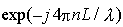 , rotazione subita durante la propagazione, con n indice di rifrazione del mezzo sede del guadagno ottico; , rotazione subita durante la propagazione, con n indice di rifrazione del mezzo sede del guadagno ottico;
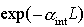 , fattore di attenuazione per effetto dell'assorbimento interno, con , fattore di attenuazione per effetto dell'assorbimento interno, con 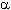 int coefficiente di assorbimento interno per unità di lunghezza; int coefficiente di assorbimento interno per unità di lunghezza;
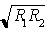 , fattori di attenuazione dovuti alla non perfetta riflettività delle facce; , fattori di attenuazione dovuti alla non perfetta riflettività delle facce;
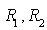 , coefficienti di riflettività 7 della faccia in z = 0 e z = L, rispettivamente. , coefficienti di riflettività 7 della faccia in z = 0 e z = L, rispettivamente.
Dall'equazione precedente, considerata in modulo e fase, si ricavano le condizioni seguenti
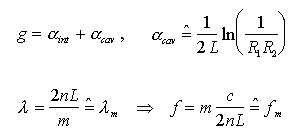
ove m è un intero arbitrario. La prima delle equazioni precedenti mostra che il guadagno ottico g deve uguagliare la somma delle perdite interne e quelle esterne (intenzionali) dovute alla non perfetta riflessività delle facce. La seconda, invece, indica che questo tipo di laser supporta in teoria un numero "infinito" di modi di oscillazione, detti longitudinali, ma in realtà, poichè g ha una curva di risposta funzione di  , la condizione di "lasing" (prima equazione) si può ottenere solo per quei valori di , la condizione di "lasing" (prima equazione) si può ottenere solo per quei valori di  m per cui g è sufficientemente alto, come indicato nella figura seguente. m per cui g è sufficientemente alto, come indicato nella figura seguente.

Fig. 2.11 - Modi di oscillazione del LASER a cavità: (a) con mezzo a guadagno ottico ideale in assenza di emissione spontanea; (b) con mezzo a guadagno ottico reale g(f) e con emissione spontanea.
Il LASER a cavità è, quindi, un dispositivo multimodo, in cui sono possibili anche modi di oscillazione trasversali relativi ad una direzione trasversale all'asse della cavità, che possono essere eliminati imponendo una condizione di cutoff. Tale condizione si realizza quando la cavità è snella (dimensione trasversale molto minore della dimensione longitudinale) rispetto al proprio asse.
2.2.3 - Laser a Semiconduttore
Quanto esposto sui LASER a cavità può essere applicato anche ai LASER a gas (He-Ne) ed a Rubino ma possono essere specializzati anche per i LASER allo stato solido a semiconduttore. La struttura di principio è mostrata di seguito.

Fig. 2.12 - Schema di principio di un LASER a cavità a semiconduttore.
È evidente che la differenza principale, rispetto alla struttura generale già esposta, è il meccanismo di pompaggio per ottenere l'inversione della popolazione. Per descriverne il funzionamento partiamo dal diagramma degli stati energetici, funzione del numero d'onda, per un semiconduttore intrinseco, mostrato di seguito.
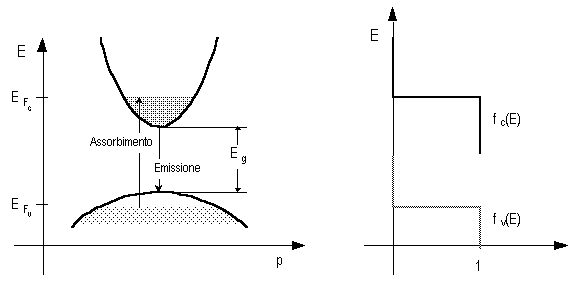
Fig. 2.13 - Diagramma e probabilità di occupazione degli stati in un semiconduttore polarizzato a 0 °K.
Per T = 0 °K, in assenza di polarizzazione esterna, la banda di valenza è piena e quella di conduzione è, invece, vuota. La distanza tra le due bande è, ovviamente, l'energia di gap. Se il semiconduttore viene polarizzato con una forte corrente di conduzione, in modo da avere forte iniezione di portatori, la banda di conduzione viene parzialmente riempita mentre quella di valenza viene parzialmente svuotata (si riempie di lacune). Ciò avviene fino al raggiungimento dei quasi-livelli di Fermi EFc ed EFv nella situazione di quasi-equilibrio, mostrato nella figura precedente. Nella situazione descritta, un fotone con energia pari a Eg = h*f0, non può venire assorbito in quanto la minima energia necessaria per l'assorbimento è EFc - EFv > Eg. L'emissione stimolata è, però, nella condizione di prevalere sull'assorbimento perchè, se h*f0 < EFc - EFv, il fotone può ugualmente stimolare una transazione dalla banda di conduzione alla banda di valenza con emissione di un fotone avente energia Eg. Affinché ciò si verifichi deve, allora, essere verificata la seguente relazione
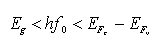
cosicché il mezzo può essere sede di guadagno ottico. Sostanzialmente si è ottenuto un sistema a quattro livelli (con E0 = EFv, E3 = EFc) grazie al meccasnismo di pompaggio adottato.
Quanto appena descritto, valido per T = 0 °K e semiconduttore intrinseco, è applicabile, almeno approssimativamente, anche per un semiconduttore drogato con T diversa dallo zero assoluto. Se la temperatura non è allo zero assoluto ed il semiconduttore è drogato, le curve della probabilità di occupazione degli stati sono più stondate e, quindi, la condizione di inversione della popolazione (equazione precedente) resta valida ma il guadagno ottico dipende anche dal drogaggio e dalla corrente I di iniezione. La condizione di inversione di popolazione si può assicurare solo con un forte drogaggio sia del materiale p che di quello n che costituiscono la giunzione p-n, contrariamente al LED nel quale l'inversione dipende dalla sola corrente anche se, per ottenere un dispositivo efficiente, si opera ancora per confinamento dell'emissione nella zona di svuotamento. Si parla in queste condizioni di giunzione degenere in cui i livelli di Fermi sono così alterati dal drogaggio da risultare all'interno della banda di valenza (parte p) e della banda di conduzione (parte n), distando più di Eg come previsto dalla condizione precedente.
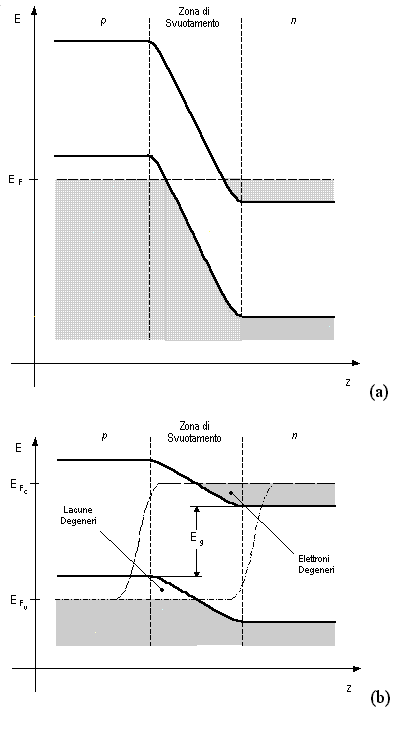
Fig. 2.14 - Giunzione p-n degenere in assenza (a) e in presenza (b) di polarizzazione diretta.
La figura precedente mostra che, se la corrente di polarizzazione è forte, cioè l'iniezione è forte, nella zona di svuotamento esistono contemporaneamente popolazioni degenerate di elettroni e lacune. Questo assicura che esiste una frequenza per cui si ha emissione stimolata e, quindi, guadagno ottico. Se il drogaggio non è forte, la condizione di inversione non può verificarsi (semiconduttore non degenere) ed il semiconduttore emette per sola emissione spontanea, il dispositivo risulta essere un LED. Inoltre l'inversione di popolazione è tanto maggiore quanto maggiore è la corrente di conduzione diretta, ovvero, è maggiore la densità di portatori iniettati (per questo prende anche il nome di LASER a semiconduttore ad iniezione).
La figura seguente riporta, per un LASER InGaAsP a 1.3  m, l'andamento del guadagno per unità di lunghezza al variare della lunghezza d'onda e per diverse concentrazioni dei portatori; si vede che al di sotto di una certa concentrazione dei portatori il guadagno è in ogni caso negativo e, quindi, non si ha amplificazione ottica. L'amplificazione si verifica, comunque, solo per un ben determinato intervallo di lunghezze d'onda, per le quali vale la relazione della condizione di inversione. La minima corrente Ith, che determina il minimo valore della concentrazione di portatori necessaria alla realizzazione della condizione di innesco, è detta corrente di soglia. Sopra il valore della corrente di soglia nel semiconduttore si ha una oscillazione di ampiezza crescente al crescere della corrente di iniezione. m, l'andamento del guadagno per unità di lunghezza al variare della lunghezza d'onda e per diverse concentrazioni dei portatori; si vede che al di sotto di una certa concentrazione dei portatori il guadagno è in ogni caso negativo e, quindi, non si ha amplificazione ottica. L'amplificazione si verifica, comunque, solo per un ben determinato intervallo di lunghezze d'onda, per le quali vale la relazione della condizione di inversione. La minima corrente Ith, che determina il minimo valore della concentrazione di portatori necessaria alla realizzazione della condizione di innesco, è detta corrente di soglia. Sopra il valore della corrente di soglia nel semiconduttore si ha una oscillazione di ampiezza crescente al crescere della corrente di iniezione.
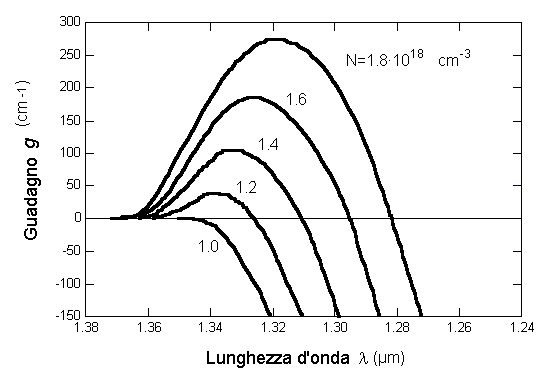
Fig. 2.15 - Guadagno per unità di lunghezza in un LASER a semiconduttore a 1.3  m. m.
Per lo stesso tipo di LASER (InGaAsP a 1.3  m) si ricavano le caratteristiche luce-corrente (L-I, dove L è riportato come potenza ottica esterna) della figura seguente. m) si ricavano le caratteristiche luce-corrente (L-I, dove L è riportato come potenza ottica esterna) della figura seguente.
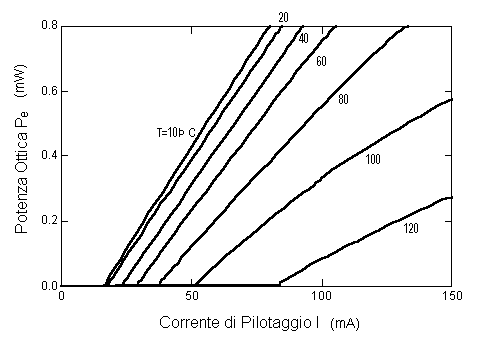
Fig. 2.16 - Caratteristiche L-I in un LASER a semiconduttore a 1.3  m. m.
Da queste caratteristiche si vede la dipendenza di Pe dalla corrente I di conduzione ed, in particolare, è evidente il fenomeno della soglia e la forte dipendenza dalla temperatura a cui si trova il LASER. È possibile dimostrare che la corrente di soglia dipende in modo esponenziale dalla temperatura: 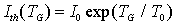 , ove I0 e T0 dipendono dal materiale. I LASER a semiconduttore usati nelle telecomunicazioni ottiche sono generalmente , ove I0 e T0 dipendono dal materiale. I LASER a semiconduttore usati nelle telecomunicazioni ottiche sono generalmente  termostatati mediante sistemi di controllo in reazione basati sull'effetto termoelettrico Peltier, per evitare instabilità delle caratteristiche di emissione. Dalla figura precedente si nota anche la buona linearità delle caratteristiche al di sopra di Ith; questo fatto rende questo tipo di LASER adatto anche per trasmissioni analogiche a modulazione d'ampiezza. Dunque sopra la Ith si può approssimare la potenza ottica esterna come termostatati mediante sistemi di controllo in reazione basati sull'effetto termoelettrico Peltier, per evitare instabilità delle caratteristiche di emissione. Dalla figura precedente si nota anche la buona linearità delle caratteristiche al di sopra di Ith; questo fatto rende questo tipo di LASER adatto anche per trasmissioni analogiche a modulazione d'ampiezza. Dunque sopra la Ith si può approssimare la potenza ottica esterna come
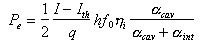
ove (I-Ith)/q è il tasso di ricombinazione dei portatori che producono fotoni per emissione stimolata mentre 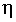 i è l'efficienza quantistica interna del dispositivo ed il fattore 1/2 tiene conto del fatto che metà dell'emissione stimolata viene persa attraverso la faccia riflettente opposta a quella utile. L'ultimo fattore mostra che in ogni sezione trasversale del materiale la frazione i è l'efficienza quantistica interna del dispositivo ed il fattore 1/2 tiene conto del fatto che metà dell'emissione stimolata viene persa attraverso la faccia riflettente opposta a quella utile. L'ultimo fattore mostra che in ogni sezione trasversale del materiale la frazione 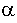 cav dei fotoni è trasmessa all'esterno mentre la frazione cav dei fotoni è trasmessa all'esterno mentre la frazione 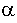 int viene assorbita all'interno del semiconduttore. int viene assorbita all'interno del semiconduttore.
Per caratterizzare i LASER a semiconduttore si introducono alcuni parametri caratteristici. Uno di essi è l'efficienza quantistica differenziale
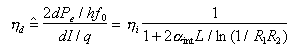
che caratterizza la maggiore o minore efficienza con cui la corrente di iniezione viene trasformata in potenza ottica. Si definisce, inoltre, l'efficienza quantistica esterna
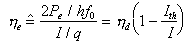
e l'efficienza totale
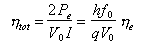 . .
In tutte le definizioni è presente un fattore 2 a moltiplicare per tenere conto della potenza ottica emessa da entrambe le facce della cavità. Nei LASER a semiconduttore, a differenza di quanto accade per i LED, l'efficienza totale può raggiungere anche valori del 50% (LASER GaAs), in quanto 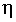 e nei LASER è molto maggiore di quella nei LED per una differenza fondamentale tra emissione stimolata e spontanea. I fotoni emessi spontaneamente nel LED si propagano in modo uniforme in tutte le direzioni mentre i fotoni emessi per stimolazione si propagano prevalentemente lungo la direzione longitudinale della cavità cosicché, mentre nel LED i fotoni che subiscono riflessione interna sono una piccola frazione del totale, nel LASER i fotoni vengono trasmessi all'esterno oppure vengono riflessi all'interno contribuendo al sostentamento dell'oscillazione ma, comunque, non percorrono traiettorie inutili. e nei LASER è molto maggiore di quella nei LED per una differenza fondamentale tra emissione stimolata e spontanea. I fotoni emessi spontaneamente nel LED si propagano in modo uniforme in tutte le direzioni mentre i fotoni emessi per stimolazione si propagano prevalentemente lungo la direzione longitudinale della cavità cosicché, mentre nel LED i fotoni che subiscono riflessione interna sono una piccola frazione del totale, nel LASER i fotoni vengono trasmessi all'esterno oppure vengono riflessi all'interno contribuendo al sostentamento dell'oscillazione ma, comunque, non percorrono traiettorie inutili.
2.2.4 - Tecniche di Fabbricazione dei LASER a Semiconduttore
Come è stato osservato per il LED, il primo passo per l'ottimizzazione del LASER è quello di ricorrere a doppie eterogiunzioni con strati di guida per un buon confinamento dell'emissione. Tale confinamento si indica anche come "verticale" riferendosi ad una disposizione in cui la giunzione è su di un piano orizzontale e l'emissione avviene longitudinalmente ad essa. Tuttavia, questi LASER ad "area estesa", poiché l'inserzione dei portatori avviene su tutta la sezione del dispositivo, non vengono usati nelle telecomunicazioni per l'impossibilità di confinare l'emissione dello strato attivo in una piccola zona orizzontale e massimizzare, così, l'efficienza di accoppiamento alla fibra. Un primo miglioramento avviene nel LASER a striscia d'ossido (Oxide-Stripe-Geometry) in cui la corrente è iniettata in una sottile striscia di semiconduttore tra due strati di ossido e, quindi, lo strato eterogeneo è attivo solo nella zona centrale (come già visto per il LED ad emissione laterale). Un miglioramento della struttura appena descritta è il LASER ridge-waveguide (figura seguente), in cui l'ossido viene depositato ai lati di una "cresta" creata rimuovendo parte del materiale della eterogiunzione; in questo modo si confina la corrente in una zona ristretta, come nel caso del LASER a striscia d'ossido ed, inoltre, si crea una discontinuità "laterale" sull'indice di rifrazione del materiale rispetto all'ossido depositato. Si origina, in questo modo, un fenomeno di guida dell'emissione che confina i fotoni nell'area di ridge.

Fig. 2.17 - LASER a semiconduttore con struttura ridge-waveguide.
Nel LASER a eterostruttura sepolta (BH, Buried Heterostructure) viene seguito un principio simile, in cui l'area attiva è confinata internamente al semiconduttore da tutti i lati. La variazione laterale dell'indice di rifrazione è più controllabile ed efficace raggiungendo un migliore confinamento laterale dell'emissione, come mostrato nella figura seguente.
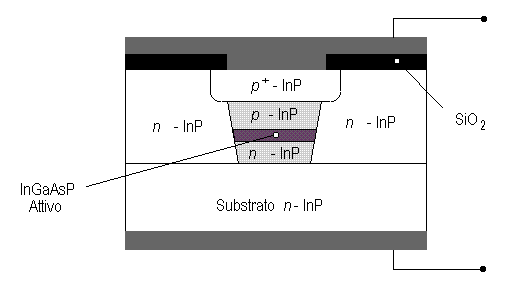
Fig. 2.18 - LASER a semiconduttore ad eterostruttura sepolta.
Il confinamento basato sulla guida per variazione dell'indice di rifrazione è molto usato nei LASER per telecomunicazioni delle ultime generazioni.
Accenniamo ai LASER a pozzo quantistico ( QW, Quantum Well). Questi LASER sono dispositivi del tipo ad eterogiunzione in cui lo strato attivo viene ridotto ad uno spessore così piccolo da essere confrontabile con la lunghezza d'onda quantistica associata ad un elettrone nel semiconduttore. Non è possibile, in queste condizioni, condurre un'analisi classica poiché vi sono effetti quantistici spiccati; in particolare, la densità degli elettroni nella banda di valenza e di lacune nella banda di conduzione assumono forme diverse da quelle previste dalla teoria classica. Tutto ciò porta come risultato macroscopico che la riduzione dello spessore dello strato attivo implica una drastica diminuzione della corrente di soglia ed, inoltre, una banda di modulazione più larga. La particolare distribuzione degli stati energetici in sottobande porta ad una modifica della curva del guadagno ottico al variare di h*f0 conducendo ad una maggiore selettività e consente di realizzare dispositivi con maggiore purezza spettrale di emissione e minore numero di modi di oscillazione. QW, Quantum Well). Questi LASER sono dispositivi del tipo ad eterogiunzione in cui lo strato attivo viene ridotto ad uno spessore così piccolo da essere confrontabile con la lunghezza d'onda quantistica associata ad un elettrone nel semiconduttore. Non è possibile, in queste condizioni, condurre un'analisi classica poiché vi sono effetti quantistici spiccati; in particolare, la densità degli elettroni nella banda di valenza e di lacune nella banda di conduzione assumono forme diverse da quelle previste dalla teoria classica. Tutto ciò porta come risultato macroscopico che la riduzione dello spessore dello strato attivo implica una drastica diminuzione della corrente di soglia ed, inoltre, una banda di modulazione più larga. La particolare distribuzione degli stati energetici in sottobande porta ad una modifica della curva del guadagno ottico al variare di h*f0 conducendo ad una maggiore selettività e consente di realizzare dispositivi con maggiore purezza spettrale di emissione e minore numero di modi di oscillazione.
2.3 - LASER a Semiconduttore Monomodo
Precedentemente abbiamo osservato che il LASER oscilla secondo una molteplicità di modi longitudinali il cui numero è limitato dalla risposta del guadagno ottico alle varie lunghezze d'onda. Abbiamo altresì visto che la distanza tra due modi è  f = c/2nL ed è dell'ordine di alcune decine fino al centinaio di GHz. La presenza di più modi di oscillazione può essere un ostacolo per la realizzazione di trasmettitori ad alta efficienza nei quali è importante che il LASER oscilli alla ben definita f = c/2nL ed è dell'ordine di alcune decine fino al centinaio di GHz. La presenza di più modi di oscillazione può essere un ostacolo per la realizzazione di trasmettitori ad alta efficienza nei quali è importante che il LASER oscilli alla ben definita  ZD, in corrispondenza del punto di zero dispersione della fibra. Non si desiderano, cioè, componenti frequenziali distanti da questo valore, come nel caso di un LASER multimodo, che possono generare fenomeni di dispersione temporale. Nei LASER monomodo vengono inibiti i modi trasversali e tutti i modi longitudinali diversi dal modo fondamentale. Quest'ultima condizione può essere raggiunta facendo sì che ZD, in corrispondenza del punto di zero dispersione della fibra. Non si desiderano, cioè, componenti frequenziali distanti da questo valore, come nel caso di un LASER multimodo, che possono generare fenomeni di dispersione temporale. Nei LASER monomodo vengono inibiti i modi trasversali e tutti i modi longitudinali diversi dal modo fondamentale. Quest'ultima condizione può essere raggiunta facendo sì che  cav sia selettiva invece che costante al variare di cav sia selettiva invece che costante al variare di  come nel caso del LASER Fabry-Pérot [lasing]. Se l'andamento della come nel caso del LASER Fabry-Pérot [lasing]. Se l'andamento della  cav presenta un minimo spiccato in corrispondenza della lunghezza d'onda cav presenta un minimo spiccato in corrispondenza della lunghezza d'onda  0 di oscillazione, la condizione di innesco dell'oscillazione può essere verificata solo per tale 0 di oscillazione, la condizione di innesco dell'oscillazione può essere verificata solo per tale  0 mentre il guadagno ottico non può compensare la perdita subita dagli altri modi. 0 mentre il guadagno ottico non può compensare la perdita subita dagli altri modi.
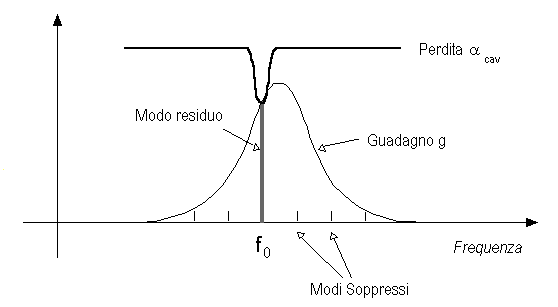
Fig. 2.19 - Soppressione dei modi in un LASER monomodo.
Un altro tipo di dispositivo monomodo è il LASER a retroazione distribuita ( DFB, Distributed Feedback), in cui la reazione ottica si realizza non con facce riflettenti ma con l'inserzione di uno strato corrugato adiacente allo strato attivo che crea una perturbazione periodica nell'indice di rifrazione. Si ha, allora, retroazione secondo il meccanismo della riflessione di Bragg 8. DFB, Distributed Feedback), in cui la reazione ottica si realizza non con facce riflettenti ma con l'inserzione di uno strato corrugato adiacente allo strato attivo che crea una perturbazione periodica nell'indice di rifrazione. Si ha, allora, retroazione secondo il meccanismo della riflessione di Bragg 8.
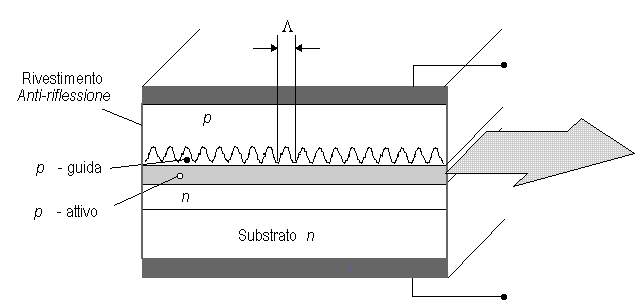
Fig. 2.20 - Struttura di principio del LASER a riflettori di Bragg (DFB).
L'interazione tra le due componenti del campo è costruttiva e, quindi, si ha reazione ottica, quando la periodicità spaziale 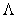 del corrugamento è tale che: del corrugamento è tale che:
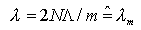
ove m è un intero arbitrario ed N è l'indice di modo del campo (ricavato dalle equazioni di Maxwell, non riportate). Il grado di accoppiamento tra l'onda progressiva e quella regressiva è maggiore per la diffrazione principale (m = 1) che per le superiori, cosicché si ottiene selettività e, quindi, monomodalità.
Un meccanismo simile avviene nel LASER a riflettori di Bragg distribuiti (DBR, Distributed Bragg Reflectors), in cui la diffrazione di Bragg viene usata per creare alle estremità del dispositivo due riflettori di riflettività selettiva.
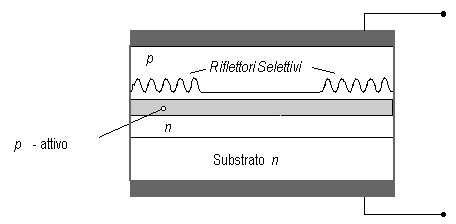
Fig. 2.21 - Struttura di principio di un LASER DBR.
La riflettività viene massimizzata scegliendo il periodo di corrugazione 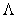 esattamente come visto per il LASER DFB. Il processo di fabbricazione di questi due tipi di LASER è raffinato e richiede alcuni stadi di crescita epitassiale ed, al fine di creare reticoli con periodicità submicrometrica, vengono anche usate tecniche olografiche. In queste tecniche olografiche il reticolo viene disegnato su uno strato di photoresist come frange di interferenza di due fasci LASER opportuni e, una volta che il reticolo è disegnato, il profilo di esso viene realizzato con crescite epitassiali multiple. La bontà di un LASER monomodo viene rappresentata con il rapporto di soppressione dei modi (MSR, Mode Soppression Ratio) esattamente come visto per il LASER DFB. Il processo di fabbricazione di questi due tipi di LASER è raffinato e richiede alcuni stadi di crescita epitassiale ed, al fine di creare reticoli con periodicità submicrometrica, vengono anche usate tecniche olografiche. In queste tecniche olografiche il reticolo viene disegnato su uno strato di photoresist come frange di interferenza di due fasci LASER opportuni e, una volta che il reticolo è disegnato, il profilo di esso viene realizzato con crescite epitassiali multiple. La bontà di un LASER monomodo viene rappresentata con il rapporto di soppressione dei modi (MSR, Mode Soppression Ratio)
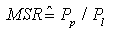
ove Pp è la potenza ottica associata al modo principale e Pl la potenza del modo laterale predominante non completamente soppresso.
Un tipo diverso di dispositivo monomodo viene costruito come dispositivo a "cavità esterna"; in esso una faccia non è riflettente e permette di accoppiare l'emissione alla cavità esterna costituita con l'aiuto di un reticolo di diffrazione. Il comportamento di questo LASER è quello di un dispositivo avente al posto della faccia trasparente una faccia riflettente con riflessività variabile con la lunghezza d'onda. Questo consente di variare, entro certi limiti, la frequenza di oscillazione variando la posizione del reticolo di diffrazione; poiché tale variazione di posizione avviene meccanicamente, per evitare di usare componenti esterni alla giunzione, talvolta, si ricorre ad un altro tipo di dispositivo, il LASER Cleaved Coupled Cavity o C 3.
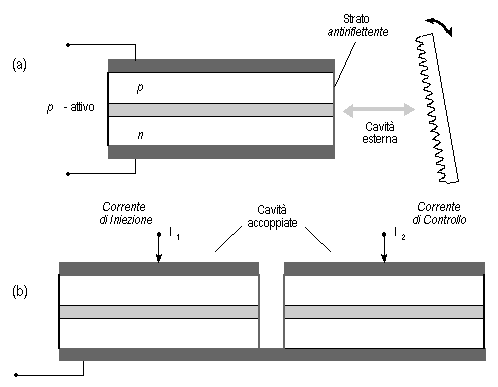
Fig. 2.22 - LASER a cavità esterna e C 3 (Cleaved Coupled Cavity).
Nel LASER C 3 l'accoppiamento avviene tra due sezioni identiche ottenute scavando un solco di larghezza 1  m, al centro della sezione di un LASER convenzionale. La presenza del solco inibisce i modi secondari e, variando la corrente di iniezione della cavità secondaria (I2), è possibile mantenere le caratteristiche di sintonizzabilità del dispositivo. Combinando il principio della cavità esterna ed i riflettori di Bragg, si ottiene un nuovo tipo di dispositivo, il LASER multisezione (o multielettrodo) DBR. m, al centro della sezione di un LASER convenzionale. La presenza del solco inibisce i modi secondari e, variando la corrente di iniezione della cavità secondaria (I2), è possibile mantenere le caratteristiche di sintonizzabilità del dispositivo. Combinando il principio della cavità esterna ed i riflettori di Bragg, si ottiene un nuovo tipo di dispositivo, il LASER multisezione (o multielettrodo) DBR.
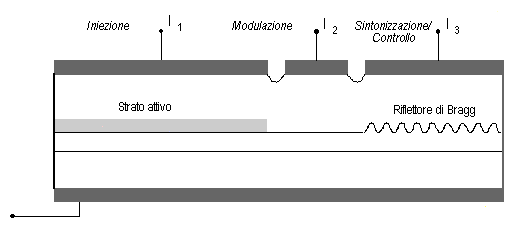
Fig. 2.23 - LASER multisezione (multielettrodo) DBR.
La prima sezione è quella attiva mentre la terza sezione costituisce l'elemento che fornisce la riflettività selettiva. Attraverso la I3, in particolare, si può variare l'indice di modo del reticolo di Bragg attraverso l'iniezione dei portatori variando, così, la frequenza di oscillazione. La sezione centrale viene usata per modulare in frequenza con una corrente esterna l'oscillazione generata.
2.4 - Banda e Fenomeni parassiti dei LASER a Semiconduttore
Dalla caratteristica luce-corrente rettilinea abbiamo dedotto che è possibile usare un LASER a semiconduttore come un modulatore di ampiezza variando la corrente di pilotaggio in modo proporzionale al segnale modulante attorno al valore medio di polarizzazione. Tale valore deve garantire il superamento della Ith per qualunque valore del segnale modulante.
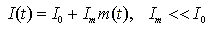
Come già fatto per il LED possiamo caratterizzare il LASER a semiconduttore in termini di risposta in frequenza per piccoli segnali. In regime sinusoidale, per piccoli segnali, si possono linearizzare le rate equations che descrivono il comportamento dinamico (al variare di t le popolazioni nei due livelli di energia) del LASER a semiconduttore attorno al punto di riposo imposto con I0. Si ricava un tipo di risposta di tipo risonante del secondo ordine, mentre nel LED si è visto che era del primo ordine, in cui la posizione della frequenza di rilassamento (picco di risonanza) dipende dal rapporto I0/Ith. Si può dimostrare che, aumentando I0, il picco si sposta verso frequenze maggiori ed il coefficiente di smorzamento aumenta. Si può, così, parlare di banda di modulazione Bm, che risulta proporzionale a [I0-Ith]1/2, con andamento quasi piatto fino ai 10 GHz.
Questa analisi per piccoli segnali non può applicarsi ai sistemi numerici realizzati con modulazioni On-Off in cui si pilota il LASER con segnali di elevata ampiezza. In pratica, il LASER viene mantenuto appena sotto Ith nello stato "Off" e pilotato con la maggiore corrente possibile sopra Ith (stato "On") al fine di ottenere la massima potenza in uscita. Non ha senso, in questi casi, parlare di linearizzare le rate equations poiché non ha senso neanche parlare di banda. Procedendo per via sperimentale si ottiene una risposta del tipo riportato nella figura seguente (tratto continuo), nel caso di un impulso di durata ristretta (0.5 ns).
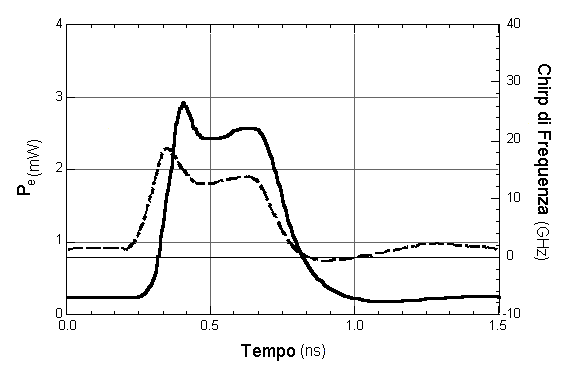
Fig. 2.24 - Chirp e oscillazione di rilassamento in un LASER con modulazione On-Off.
L'andamento di Pe mette in luce una sorta di "limitazione in banda", più precisamente una, limitazione del tempo di risposta, poiché l'impulso non ha fronti ripidi in salita ed, inoltre, presenta una dissimmetria tra fronte in salita e fronte in discesa per fenomeni di comportamento non lineare.
Nella stessa figura è mostrata un'altra caratteristica della risposta in frequenza di un LASER a segnali di grande ampiezza chiamata frequency chirping (linea tratteggiata). Il fenomeno del "chirp" si presenta per una brusca e ampia variazione della corrente di pilotaggio in cui il LASER attraversa situazioni di forte squilibrio dovute alla variazione dell'indice di rifrazione del semiconduttore al variare del grado di iniezione. In queste condizioni si produce una rapida modulazione di fase dell'oscillazione generata, per cui la frequenza istantanea di oscillazione varia, nel transitorio, rispetto al valore di regime stazionario f0. Lo spostamento della frequenza istantanea è causa di un allargamento dello spettro dell'impulso (in figura di durata 0.5 ns come in precedenza) rispetto al valore teorico, dando luogo a degradazione nelle prestazioni in termini di BER (Bit Error Rate) di un sistema numerico in cui è usato un LASER di questo tipo.
Un LASER è, idealmente, un generatore di segnale sinusoidale a frequenza ed ampiezza fissate (oscillatore ideale) ma, in realtà, produce un segnale non esattamente sinusoidale, come ogni oscillatore, caratterizzato da una densità spettrale di potenza differente da quella ideale a riga singola. Infatti, un LASER presenta fluttuazioni non trascurabili della frequenza, della fase e dell'ampiezza del segnale generato, sia a breve che a lungo termine. Sul lungo termine la frequenza di oscillazione del LASER varia per effetto del rumore flicker, provocando lente fluttuazioni della frequenza f0 nominale caratterizzate da una densità spettrale del tipo 1/(f) 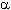 , con , con 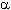 compreso tra 1 e 2. compreso tra 1 e 2.
L'instabilità termica è un'altra causa di queste variazioni di frequenza e può essere minimizzata  termostatando il LASER. L'ordine di grandezza della sensibilità dell'oscillazione a variazioni di temperatura per i LASER attuali è di qualche decina di GHz/K, tipicamente 20 GHz/K. termostatando il LASER. L'ordine di grandezza della sensibilità dell'oscillazione a variazioni di temperatura per i LASER attuali è di qualche decina di GHz/K, tipicamente 20 GHz/K.
La fonte principale di disturbo resta, in ogni caso, l'emissione spontanea contribuendo con una molteplicità di componenti di fase (e di ampiezza) aleatorie, al campo utile prodotto dalla emissione stimolata. Per caratterizzare l'effetto apportato dall'emissione spontanea, considerando il valore medio della potenza ottica generata Pe, si esprime la potenza istantanea come
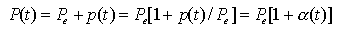
ove 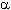 (t) è la fluttuazione di potenza normalizzata a valore medio nullo dell'emissione spontanea chiamata rumore relativo d'intensità (RIN, Relative Intensity Noise). Per caratterizzare in modo pratico il RIN viene fornito il rapporto segnale-rumore (SNR) del LASER, definito come il valore in dB di Pe/ (t) è la fluttuazione di potenza normalizzata a valore medio nullo dell'emissione spontanea chiamata rumore relativo d'intensità (RIN, Relative Intensity Noise). Per caratterizzare in modo pratico il RIN viene fornito il rapporto segnale-rumore (SNR) del LASER, definito come il valore in dB di Pe/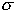 p, con p, con 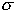 p2 la varianza della fluttuazione p(t), si ottiene p2 la varianza della fluttuazione p(t), si ottiene
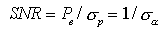
ove 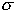 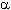 è la varianza del RIN stesso. è la varianza del RIN stesso.
Supponendo che il modo del LASER presenti polarizzazione lineare, così da potersi usare una notazione scalare con riferimento alla direzione di polarizzazione e supponendo di poter trascurare il RIN, il campo generato dal LASER alla superficie della faccia emittente della cavità non è sinusoidale per effetto dell'emissione spontanea. L'inviluppo complesso del campo sulla superficie è, allora, del tipo
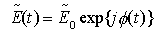
ove .gif) è un processo aleatorio detto rumore di fase. Il rumore di fase è un processo aleatorio detto rumore di fase. Il rumore di fase .gif) viene modellato come un processo di Wiener-Lévy ad incrementi gaussiani; ciò equivale a dire che il rumore di frequenza viene modellato come un processo di Wiener-Lévy ad incrementi gaussiani; ciò equivale a dire che il rumore di frequenza
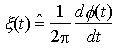
è ipotizzato un processo stazionario gaussiano bianco con densità spettrale di potenza 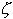 0. 0.
Da considerazioni più approfondite si può ricavare che 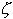 0 0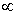 RSP/Pe e che la densità spettrale di emissione del LASER è RSP/Pe e che la densità spettrale di emissione del LASER è
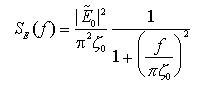
la cui forma viene detta Lorentziana. Ricavando la larghezza di emissione FWHM 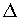 f si trova f si trova
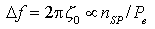
che rappresenta la larghezza di linea del dispositivo.

Fig. 2.25 - Spettro di potenza di un LASER, con rumore di frequenza bianco, a 1.5  m. m.
LASER con piccola larghezza di linea garantiscono un grado di coerenza temporale maggiore e sono, quindi, componenti di maggior pregio. Negli anni si è passati da larghezze di linea dell'ordine delle decine di GHz dei LASER delle prime generazioni a larghezze di linea dell'ordine del MHz per le più recenti generazioni di LASER DFB multielettrodo, questi ultimi progettati specificatamente per sistemi di comunicazioni "coerenti" in cui, come vedremo nel Cap. 4.4, il requisito di coerenza temporale (monocromaticità) dell'emissione è essenziale.
|
|

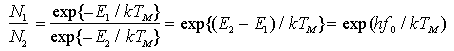
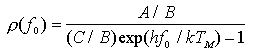 .
.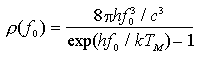
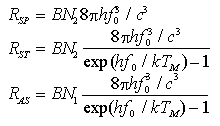

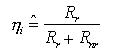
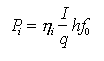 .
.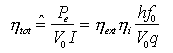
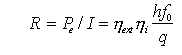 .
.



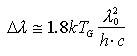 .
.