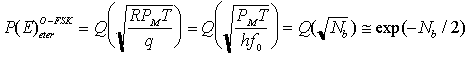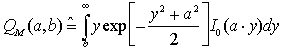Nel capitolo precedente è stata fatta un'analisi del progetto del front-end di un ricevitore per segnali ottici. È necessario, adesso, passare ad una descrizione più approfondita delle tecniche di modulazione e della struttura dei relativi ricevitori per comunicazioni numeriche tramite fibra ottica, senza trascurare le prestazioni offerte dai medesimi. Nell'analisi proposta di seguito verrà indicata con Rb la cadenza di trasmissione dell'informazione (bit/s) corrispondente ad un periodo di clock della sorgente pari a T = 1/Rb.
Nella stessa figura è riportato anche un possibile circuito di controllo a reazione (a dinamica lenta) che mantiene la potenza media Pe del LASER costante. La buona linearità della caratteristica Pe-I di tali dispositivi garantisce che l'andamento temporale della potenza prodotta dal modulatore ricalca con fedeltà la forma d'onda della corrente elettrica associata alla trasmissione di un bit uguale al valore logico "1" o al valore logico "0", in generale detti simboli. La modulazione d'intensità più semplice da realizzare è la cosiddetta On-Off Keying (OOK), in cui il LASER viene mantenuto a potenza costante per l'intervallo di bit T in cui si desidera trasmettere il simbolo "1"; viceversa viene completamente spento, ancora nell'intervallo di bit T, per trasmettere il simbolo "0". La potenza ottica utile del segnale incidente sul fotorivelatore, nell'ipotesi di poter trascurare la dispersione e l'attenuazione dovute alla fibra, è del tipo
ove bk è il k-esimo simbolo trasmesso, PM è la potenza ottica di picco ricevuta e p(t) è un impulso rettangolare di ampiezza unitaria e durata T. Nel seguito faremo l'ipotesi che, come di consueto, {bk} sia una successione di variabili aleatorie mutuamente indipendenti che assumono con probabilità 1/2 i valori appartenenti all'alfabeto dei simboli trasmesso, in questo caso {0, 1}.
Supponiamo che la trasmissione di un segnale IM avvenga per simboli isolati (one-shot) e vediamo come ricevere tali simboli in modo ottimale. In questo tipo di trasmissioni, nel k-esimo intervallo di bit, il trasmettitore invia uno dei due possibili segnali definiti per kT
in cui P(bk)0(t) è la forma d'onda associata ai simboli bk trasmessi; per un segnale OOK, evidentemente, si ha P(0)0(t) = 0, P(1)0(t) = PM, 0
in cui NT è il numero totale di impulsi di corrente nati nell'intervallo [0, T). Tale processo, in generale non omogeneo, è caratterizzato dalle due diverse intensità
a seconda che il simbolo trasmesso valga, rispettivamente, "0" o "1".
L'aleatorietà del processo di fotorivelazione implica che il vettore I è un vettore aleatorio caratterizzato da una certa densità di probabilità fI(i). Il ricevitore con strategia MAP, tra i due simboli possibili, sceglie come valore stimato del simbolo trasmesso quello avente la massima probabilità a posteriori PAP. PAP è definita come la probabilità dei due possibili valori di simbolo condizionato al particolare valore osservato assunto dal vettore I
Se con p0 = Pr{b0 = 0} e p1 = Pr{b0 = 1} (ove b0 è il simbolo trasmesso nell'intervallo iniziale) si indicano le probabilità a priori di presentazioni dei simboli, rispettivamente "0" ed "1", sappiamo dal teorema di Bayes che vale la relazione
ove il termine a denominatore non dipende dal valore di simbolo. Per questo il denominatore della relazione precedente non interviene sulla decisione e, quindi, la regola MAP può esprimersi come:
ove
La funzione
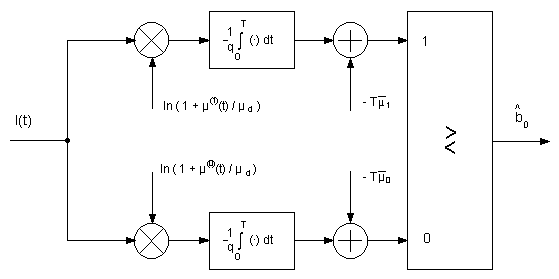
che ricalca da vicino lo schema del ricevitore ottenuto nel caso di canale additivo Gaussiano (ricevitore a correlatori, o a filtri adattati, con pesaggio delle uscite per tenere conto delle diverse energie dei segnali trasmessi, e successiva rete che determina il massimo di tali quantità).
per cui la legge di decisione può esprimersi come
tipica di un ricevitore a soglia
Questo risultato estremamente semplice deriva dal fatto che le relazioni precedenti sono ricavate nell'ipotesi che la banda del fotorivelatore sia molto maggiore della velocità di trasmissione (Bf*T >> 1). In queste condizioni l'impulso di corrente elementare h(t) del dispositivo è assimilabile ad una funzione impulsiva avente integrale pari a q, ovvero h(t)
che, nell'ipotesi di efficienza quantistica unitaria, è anche il numero di fotoni che hanno interagito con il fotorivelatore.
In esso si decide che il simbolo stimato è uguale ad 1, come indica anche la legge di decisione precedente, non appena il ricevitore riesce a contare almeno un fotone nell'intervallo di segnalazione T.
Per calcolare la probabilità di errore del ricevitore a conteggio di fotoni basta osservare che NT condizionatamente al valore di b0 = n è una variabile aleatoria distribuita secondo Poisson, con parametro
Utilizzando, allora, il teorema della probabilità totale e nell'ipotesi che la corrente di buio sia assente, si ha
e, quindi, in assenza di potenza ottica incidente non è possibile commettere alcun errore sul simbolo 0 poiché, in tal caso, non può essere contato alcun fotone. Nel caso opposto si ha
ed, in definitiva, si ottiene che la probabilità di errore è pari a
PMT/hf0, in particolare, è il numero di fotoni rivelati in media in un intervallo di bit in cui viene trasmesso un simbolo pari ad uno nel caso in cui
ed esprimere la probabilità di errore nella forma
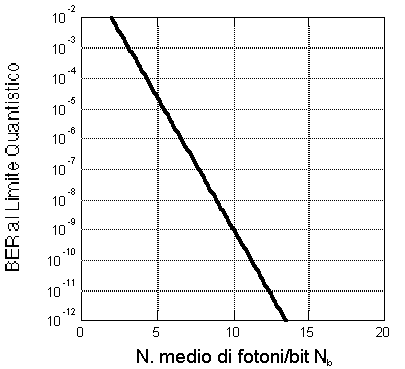
che prende il nome di limite quantistico (Quantum Limit) alle prestazioni del ricevitore DD per trasmissioni IM-OOK. Tale limite si riferisce al fatto che nel calcolo di P(E) è stata trascurata ogni fonte di non-idealità del ricevitore (
Sappiamo che la sensibilità del ricevitore è quel valore di potenza ottica media ricevuta
da cui, considerando che la potenza media trasmessa in una trasmissione OOK è PM/2, si ricava
Quest'ultima relazione fornisce una sensibilità teorica al limite quantistico per un tale ricevitore ideale e, nell'ipotesi di Rb = 2.5 Gbit/s con
Le prestazioni del ricevitore a conteggio di fotoni per trasmissioni OOK sono degradate, rispetto al quantum limit, dai disturbi dovuti alla corrente di buio del fotorivelatore ed al rumore termico del front-end del ricevitore. La corrente in ingresso al ricevitore è, infatti, costituita da tre componenti
ove ISH(t) è la corrente di fotorivelazione, Id(t) è la corrente di buio e IT(t) è la corrente dovuta al rumore termico. Se il valore medio della corrente di buio è Id = q*
ove N è una variabile aleatoria di Poisson con parametro
e, quindi,
Derivando quest'ultima rispetto a
in questo caso si ottiene P(E|b0 = 0) = P(E|b0 = 1) e la BER vale
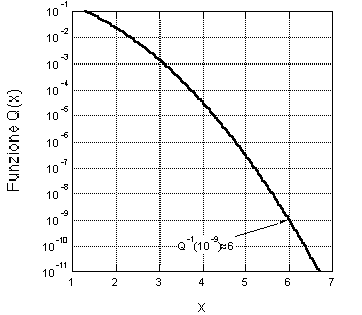
Imponendo BER = 10 -9 è possibile ricavare la sensibilità del ricevitore; utilizzando il grafico precedente si ricava immediatamente che deve aversi x
Da questa relazione si ricava che, quando il rumore termico è trascurabile (
Nel caso generale si ottiene per sensibilità del ricevitore semplicemente la somma delle espressioni parziali viste adesso
che permette di ricavare un valore approssimato della sensibilità del ricevitore in ogni condizione.
Nel caso in cui si utilizzi un ricevitore DD per segnali OOK con APD, l'analisi appena vista è più complessa poiché, in questo caso, si necessita di una caratterizzazione statistica completa dei guadagni di fotorivelazione Mk che compaiono nell'espressione del processo di Poisson marcato IAPD(t). Tale caratterizzazione si ricava attraverso la risoluzione di un'equazione differenziale cui soddisfa la funzione caratteristica di Mk, ricavata da un modello fisico dello APD.
e
Quest'ultima consente di fare considerazioni simili a quelle viste riguardo il rapporto segnale-rumore: quando il rumore termico domina, lo APD porta ad un miglioramento della sensibilità del fattore M, mentre quando il rumore shot è dominante c'è un peggioramento del fattore F. Per valori tipici della responsivity dei fotodiodi e delle cifre di rumore degli amplificatori elettrici, il miglioramento ottenibile con un APD in II o III finestra rispetto all'uso di un diodo p-i-n è dell'ordine di 6-8 dB.
Nel progetto di un sistema di trasmissione IM/DD, al di là delle considerazioni teoriche appena fatte, si devono tenere presenti alcuni fattori pratici che possono influenzare la bontà delle prestazioni del collegamento. Ad esempio, nel trasmettitore può essere conveniente mantenere il livello di potenza ottica P(0)T trasmessa in corrispondenza di un simbolo pari a "0", al di sopra dello zero. In questo modo il LASER di trasmissione viene mantenuto sopra soglia evitando problemi di chirp, di cui abbiamo già parlato. Tale accorgimento, quantificato attraverso il rapporto di estinzione
porta ad un peggioramento della BER del ricevitore; in particolare, perchè tale peggioramento si riveli praticamente trascurabile, bisogna assicurarsi che il rapporto di estinzione sia più piccolo del fattore 0.05.
cosicché la valutazione del degrado di prestazioni dovute al jitter è semplificata.
cui corrisponde un istante di campionamento ottimo t = 0. Se il filtro di ricezione nel ricevitore con fotorivelatore ideale è tale da limitare il rumore di fotorivelazione senza alterare la forma d'onda a coseno rialzato, allora, campionando con un piccolo offset
Un errore all'istante di campionamento pari a
rispetto al caso di assenza di jitter. Mediando su
Inoltre, la varianza delle fluttuazioni di corrente indotte dal jitter risulta
Considerando queste fluttuazioni di corrente una variabile aleatoria Gaussiana ed inserendo le precedenti relazioni nell'espressione della sensibilità del ricevitore in regime dominato dal rumore termico, si ottiene
che consente la valutazione della degradazione di sensibilità
e, quindi, dividendo membro a membro le due relazioni precedenti si ottiene
Poiché in assenza di jitter si ha che
si può scrivere che
ed infine
La figura seguente mette in evidenza come tale perdita risulti trascurabile quando
La trasmissione e ricezione IM/DD descritta in precedenza è un metodo efficiente e molto semplice per la trasmissione di informazione numerica su fibra; allo stesso tempo la rivelazione diretta di segnali ottici modulati in intensità è alquanto rozza se confrontata con gli schemi consueti di trasmissione numerica nel campo della radiotecnica: gli schemi di modulazione ottica, ad esempio, basati sulla variazione di fase e/o frequenza di una portante sinusoidale non sono implementabili attraverso il semplice schema di trasmissione IM/DD. Ciò è dovuto alla intrinseca insensibilità del fotorivelatore a variazioni di fase o di frequenza del segnale incidente. I sistemi IM/DD costituiscono l'unica alternativa quando la sorgente luminosa è un LED, che è caratterizzato da una emissione altamente non coerente a banda larga. I moderni LASER a semiconduttore monomodo a basso rumore di fase, impiegati anche nei più moderni sistemi IM/DD per minimizzare i fenomeni di dispersione intermodale, sono caratterizzati da un'alta coerenza temporale dell'emissione e, dunque, possono essere visti come "oscillatori sinusoidali ottici". È lecito, in tal caso, domandarsi se sia possibile progettare sistemi di trasmissione diversi dagli IM/DD in cui si riesca a modulare e rivelare la fase e/o la frequenza del segnale lanciato in fibra: questi sistemi sono comunemente indicati come sistemi coerenti 11. La prima caratteristica fondamentale su cui si basa il progetto dei sistemi ottici coerenti, già visto nel capitolo sulle sorgenti luminose, riguarda il lato trasmettitore:
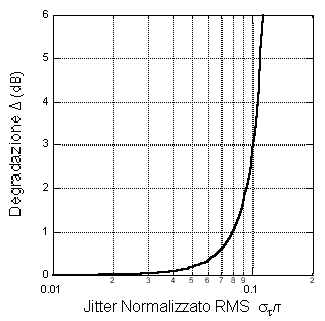
In figura sono rappresentati schematicamente i segnali risultanti dalle modulazioni numeriche elementari di fase (PSK, Phase Shift Keying), ampiezza (ASK, Amplitude Shift Keying) e frequenza (FSK, Frequency Shift Keying) per una particolare successione, o pattern, di dati.
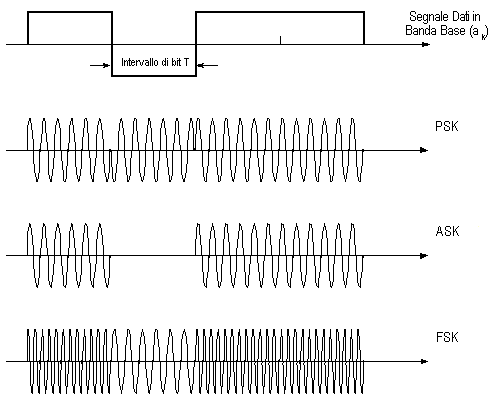
In figura è schematizzata la parte frontale semplificata di un ricevitore coerente: il segnale ricevuto viene combinato con il segnale di un LASER locale, usato come un "oscillatore locale" di un familiare schema eterodina della radiotecnica, per consentire la rivelazione di segnali modulati in fase e/o frequenza, come vedremo tra breve. Il ricevitore coerente si distacca nettamente dallo schema del ricevitore DD, poiché vengono effettuate operazioni elementari di elaborazione ottica del segnale ricevuto prima della fotorivelazione del segnale stesso.
ove f0 è la frequenza associata alla lunghezza d'onda
Sappiamo che il fotorivelatore è sensibile alla potenza ottica istantanea del segnale incidente e che tale potenza è proporzionale, secondo un fattore determinato dalla conformazione dell'area del dispositivo, al modulo quadro del campo elettrico incidente ER(t) risultante dalla combinazione dei campi forniti con le relazioni precedenti
Supponendo che il campo ricevuto ed il campo locale siano entrambi polarizzati linearmente e che lo stato di polarizzazione (SOP, State of Polarization) di entrambi i campi sia allineato (campi paralleli), ci si può riferire alla comune direzione di polarizzazione e passare alla notazione scalare
Tenendo conto, a questo punto, del legame tra potenza e campo elettrico si ha
ove PM è la potenza di picco utile del segnale modulato incidente sul fotorivelatore e PL è la potenza utile del LASER locale. Dalla relazione precedente è possibile ricavare il valore medio statistico del processo impulsi di Poisson non stazionario che rappresenta la corrente di fotorivelazione
Eliminando i termini alle frequenze ottiche 2f0, 2fL, f0 + fL a cui il fotorivelatore non è sensibile (sono al di fuori della banda di sensibilità del fotorivelatore), si ottiene
ove fIF = f0 - fL è la frequenza intermedia generalmente scelta nella banda delle microonde ed è, quindi, dell'ordine di qualche GHz. Eliminando anche le componenti in banda base, si ha
che mostra come la modulazione di ampiezza/angolo impressa sul segnale ottico ricevuto viene trasferita inalterata su di un segnale elettrico la cui frequenza portante è nell'ambito delle microonde e che, quindi, può essere demodulato secondo le tecniche standard della radiotecnica.
La frequenza intermedia fIF, come si vede, su cui il demodulatore dati elettrico opera, è determinata dalla differenza delle frequenze di trasmissione e del LASER locale e, quindi, il ricevitore coerente è intrinsecamente agile in frequenza (in grado di ricevere trasmissioni su diverse lunghezze d'onda), purché il LASER locale sia sintonizzabile. Molti dispositivi LASER si prestano a questo scopo, dando la possibilità di variare la sintonia del ricevitore su di un intervallo di lunghezza d'onda ampio. Il ricevitore DD, non essendo in alcun modo selettivo in frequenza, non è in grado di discriminare trasmissioni a diverse lunghezze d'onda coesistenti sulla medesima fibra se non viene preceduto da opportuni componenti ottici (filtri ottici) che presentano caratteristiche di sintonizzabilità e selettività inferiori a quelle ottenibili con la rivelazione coerente.
Con riferimento ad una trasmissione numerica con periodo di simbolo T, nelle applicazioni pratiche, l'ipotesi PL >> PM comporta anche che l'ipotesi di grande intensità 12 del rumore di fotorivelazione, di cui avevamo già detto in precedenza, è verificata, cosicché si può fare anche l'ipotesi semplificativa di statistiche Gaussiane per il processo di rumore. Il segnale elettrico, in conclusione, nello stadio a frequenza intermedia di un ricevitore coerente eterodina, eliminate le componenti in banda base, risulta pari a
ove i(t) è, in definitiva, un processo Gaussiano bianco con densità spettrale di potenza Si = qRPL, indipendente dal segnale.
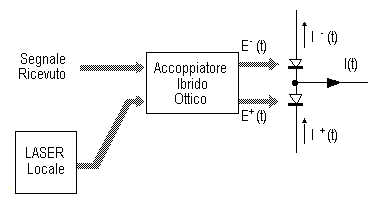
Nell'ibrido ottico, chiamato anche accoppiatore a -3 dB, il segnale ricevuto viene suddiviso con un rapporto di potenza bilanciato (0.5/0.5) sui due rami ed accoppiato ad un segnale proveniente dal LASER locale prima della rivelazione; il segnale del LASER locale viene parimenti suddiviso nello stesso rapporto di potenza, all'interno dello stesso componente e prima della combinazione con il segnale ricevuto ma con un opportuno sfasamento tra i due rami in modo da presentarsi all'uscita dell'accoppiatore sulla linea superiore in controfase rispetto alla linea inferiore. I segnali incidenti sui due fotorivelatori sono, dunque, dati da
ed i due fotorivelatori sono connessi in modo che la corrente di fotorivelazione totale I(t) risulti la differenza delle due correnti di fotorivelazione parziali
Supponendo un perfetto bilanciamento della responsivity dei due fotodiodi (R+ = R- = R), la componente media utile rivelata della corrente totale, trascurando i termini a frequenze ottiche, è pari a
ovvero i termini in banda base vengono spontaneamente a cancellarsi. Per il rumore di fotorivelazione il disturbo totale i(t) è costituito dalla differenza di due contributi i+(t) ed i-(t) statisticamente indipendenti (perché prodotti da due operazioni di fotorivelazione indipendenti) ed aventi densità spettrale di potenza pari a metà di quella relativa al processo i(t) nel combinatore sbilanciato, poiché generati dalla fotorivelazione di segnali aventi potenza ottica dimezzata dall'accoppiatore. Ne segue, immediatamente, che il disturbo totale ha una descrizione statistica del tutto equivalente a quella del disturbo nel caso del front-end sbilanciato; ci siamo così ricondotti alla situazione standard per la radiotecnica di segnale passa-banda con modulazione di ampiezza/angolo e rumore additivo Gaussiano bianco. In teoria, le tecniche per il progetto ottimo di ricevitori per trasmissione numerica in questo ambiente possono essere applicate al caso attuale senza alcuna modifica.
Per valutare le prestazioni in termini di BER che i sistemi coerenti sono in grado di offrire, cominciamo ad esaminare un caso che ha il diretto analogo nel campo dei sistemi IM/DD: la modulazione OOK. Tale modulazione nei sistemi coerenti viene più spesso indicata come modulazione ASK. Nella espressione generale del segnale modulato ASK, indicando con p(t) la forma dell'impulso trasmesso e con bk i simboli trasmessi (bk = 0, 1), si deve porre
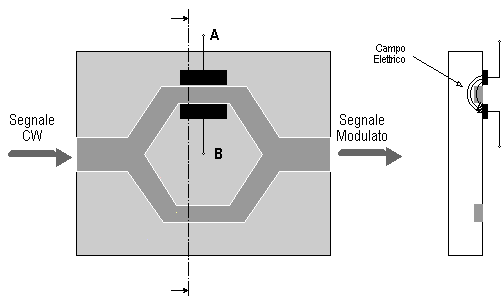
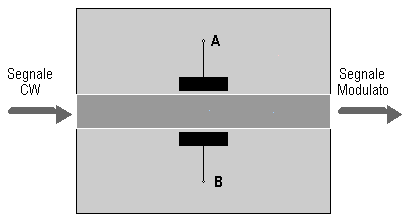
A differenza del modulatore visto per la OOK per sistemi DD, per il quale il LASER viene acceso o spento variando la corrente di pilotaggio, provocando fenomeni di chirp e perdita di coerenza temporale intollerabile per un sistema coerente, nel modulatore coerente ASK si ricorre ad un LASER ad onda continua (CW, Continuous Wave) non modulato e ad un modulatore esterno. Il modulatore esterno, che ha il compito di arrestare o trasmettere il segnale, è un componente elettro-ottico, in quanto il comando di accensione/spegnimento è dato dal segnale dati elettrico, che può essere realizzato mediante l'interferometro di Mach-Zehnder miniaturizzato, mostrato di seguito.
In assenza di tensione tra gli elettrodi A e B, i segnali nelle due guide d'onda miniaturizzate realizzate con tecnica integrata su di un substrato di Niobato di Litio, che costituiscono i due rami dell'interferometro ,si combinano in fase restituendo in uscita il medesimo segnale, in teoria, presente all'ingresso prima della suddivisione; in pratica si hanno perdite da inserzione del modulatore attorno al dB. In presenza di un'opportuna tensione VAB (alcuni Volt), i due cammini si ricombinano in opposizione di fase, provocando la cancellazione del segnale. Lo sfasamento si verifica poiché alcuni materiali hanno indice di rifrazione variabile al variare del campo elettrico cui sono sottoposti (effetto Pockel o elettro-ottico); questo fenomeno consente di sfasare il campo elettrico del segnale sul ramo superiore per ottenere l'effetto desiderato ed ottenere un rapporto di estinzione r, per un buon modulatore siffatto, attorno ai 20 dB.
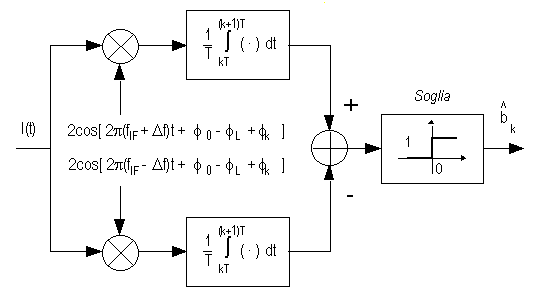
ove, nell'ipotesi PL >> PM e fotorivelatore a banda larga, i(t) è un processo Gaussiano bianco con d.s.p. Si(f) = qRPL. La teoria del ricevitore ottimo su canale AWGN (Additive Gaussian White Noise) prevede di usare il demodulatore sincrono con recupero perfetto del sincronismo di fase della portante a frequenza intermedia e filtro adattato all'impulso p(t) (integratore), come mostrato nella figura seguente in cui
Nell'ipotesi fIF >> 1/T possiamo scrivere direttamente l'espressione della probabilità di errore di tale ricevitore sincrono dai risultati standard della trasmissione passa-banda in un canale AWGN
Introducendo il numero medio di fotoni per bit Nb = PMT/2hf0 e supponendo unitaria l'efficienza quantistica del fotorivelatore p-i-n utilizzato, si ha
Poiché Q(x) si può approssimare come e-(x2/2) quando x >> 1, la relazione precedente può essere riscritta come
che, confrontata con il corrispondente limite quantistico del ricevitore DD, denuncia una perdita di 6 dB di sensibilità.
in cui, è evidente che, per evitare attenuazioni o perdita totale di segnale quando
con una perdita di soli 3 dB rispetto al limite quantistico e con guadagno di 3 dB rispetto al ricevitore eterodina. Questo risultato può spiegarsi pensando che il rumore di fotorivelazione i(t) ha in entrambi i casi la stessa densità spettrale di potenza, mentre il segnale omodina in banda base ha potenza doppia del segnale eterodina in banda passante. La complessità di un ricevitore coerente, naturalmente, è maggiore di quella relativa ad un ricevitore DD che nel caso appena visto richiede un demodulatore sincrono nella parte elettrica e nella parte frontale ottica. È necessario, quindi, sfruttare al meglio la capacità del ricevitore coerente di rivelare segnali modulati d'angolo che, in generale, offrono prestazioni migliori dello ASK. Consideriamo il caso di un segnale trasmesso modulato in fase secondo lo schema BPSK (Bi-Phase Shift Keying)
con le stesse notazioni viste per il segnale ASK. Il modulatore PSK coerente può essere realizzato da un LASER CW e da un modulatore esterno elettro-ottico (effetto Pockel) in Niobato di Litio (LiNbO3), come mostrato di seguito.
Applicando una opportuna tensione agli elettrodi di controllo il segnale ottico nella guida viene sfasato di
ove ak = 2bk-1 è la versione polare (ak = +1, -1) del simbolo bk (bk = 0, 1). Il demodulatore PSK ottimo è ancora uno schema sincrono con recupero della portante a frequenza intermedia, ed è riportato nella figura seguente.
Nel caso di perfetta sincronia della portante si trova che il valore della probabilità di errore per tale ricevitore è
coincidente con la P(E)ASKomo e peggiore di 3 dB rispetto al limite quantistico del sistema OOK/DD. Si noti che, per il segnale PSK in cui il LASER è attivo alla stessa potenza sia quando bk = 0 che quando bk = 1, si ha Nb = PMT/hf0. Di conseguenza la P(E)ASKomo coincide con la P(E)PSKeter a parità di numero medio di fotoni per bit Nb, cioè a parità di potenza media del LASER di trasmissione. Dal confronto dei due sistemi a parità di potenza di picco PM ricevuta, vediamo che il PSK eterodina è, in realtà, migliore di 3 dB (sarà più chiaro quando vedremo le curve della BER) rispetto allo ASK omodina, e il limite quantistico della OOK/DD, con lo stesso vincolo sulla potenza di picco, coincide proprio con la P(E)PSKeter appena vista.
Supponendo
che risulta approssimativamente coincidente con il limite quantistico della OOK/DD a parità di potenza media di trasmissione e migliore di quest'ultima di 3 dB a parità di potenza di picco. Prestazioni intermedie tra la ASK e la PSK sono fornite dalla modulazione FSK, ottenuta come modulazione diretta del LASER di trasmissione, il cui segnale trasmesso si ottiene ponendo
che mette in luce come nel generico intervallo di segnalazione [kT, (k + 1)T) venga trasmesso uno tra due toni a frequenza f0 +
Nel campo ottico viene più spesso usata la FSK ortogonale, in cui i due toni di segnalazione sono ortogonali sull'intervallo di segnalazione; ciò si verifica quando 2
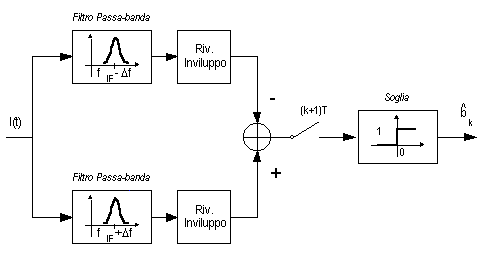
In questo caso si trova la probabilità di errore del ricevitore sincrono a due rami, mostrato nella figura precedente, pari a
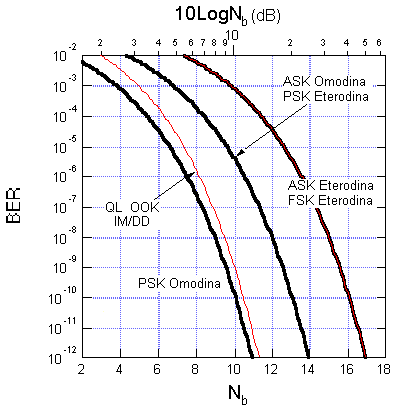
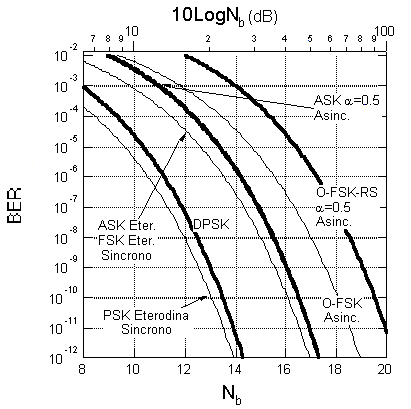
che risulta intermedia, a parità di potenza di picco, tra ASK e PSK. Chiaramente la demodulazione omodina della FSK non è possibile. Le prestazioni dei diversi schemi di modulazione e demodulazione coerente sono riassunte nella tabella seguente.
Le corrispondenti curve di BER, in funzione del numero medio di fotoni per bit Nb, sono tracciate nella figura seguente, ove sono confrontate con il limite quantistico della OOK con ricevitore DD ideale.
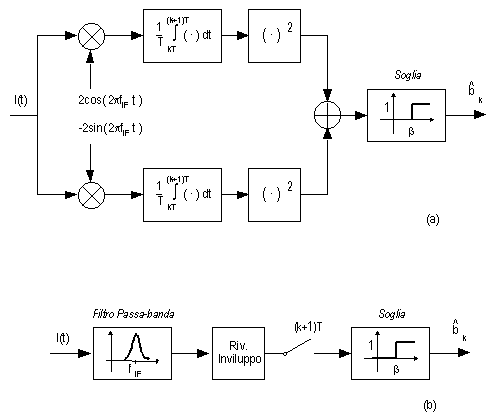
Le difficoltà di realizzazione di un demodulatore eterodina sincrono alla frequenza fIF si possono aggirare mediante l'implementazione di schemi di demodulazione asincroni che non necessitano del recupero della portante di trasmissione. In teoria il ricevitore asincrono è ottimo quando si assume incognito l'angolo di fase iniziale del segnale ricevuto.
in cui
e I0(*) è la funzione di Bessel modificata di prima specie ed ordine zero. Si osserva che, mentre nel ricevitore sincrono la soglia normalizzata è fissata al valore
Il peggioramento delle prestazioni è, quindi, modesto a fronte di una semplificazione del ricevitore che non richiede circuiti ad aggancio di fase.
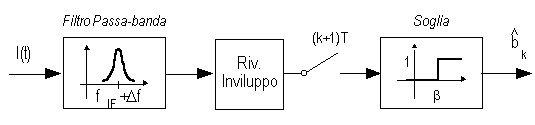
La perdita di sensibilità del ricevitore asincrono rispetto al sincrono è, anche in questo caso, intorno ai 0.5 dB. A parità di potenza di picco, come per i ricevitori sincroni, il ricevitore FSK ha una sensibilità migliore di 3 dB rispetto al corrispondente ricevitore asincrono per ASK. La FSK ortogonale viene, talvolta, demodulata con uno schema asincrono sub-ottimo a singolo ramo ottenuto dal precedente sopprimendo la rivelazione di uno dei sue toni e confrontando l'uscita del rivelatore di inviluppo con una soglia non nulla ma pari al consueto valore normalizzato
Ciò equivale a trattare la FSK come una sorta di ASK con frequenza portante coincidente con il tono di segnalazione rivelato, ignorando la presenza del tono ortogonale trasmesso in corrispondenza dei simboli "0". Il ricevitore a ramo singolo coincide, allora, con lo schema per ASK e le prestazioni in termini di BER peggiorano di 3 dB rispetto al demodulatore a doppio ramo. Lo schema a singolo ramo fornisce, infatti, una probabilità di errore pari a
che, a parità di potenza di picco, coincide esattamente con la BER del ricevitore asincrono per ASK. La perdita di 3 dB del demodulatore a singolo ramo è, ovviamente, compensata dalla maggiore semplicità strutturale di tale schema.
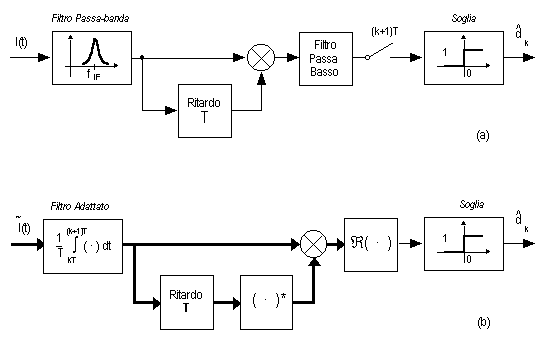
Il generico simbolo di linea è identico al precedente se il corrispondente simbolo di sorgente assume il valore "1"; viceversa se il simbolo di sorgente vale "0". È possibile, in questo caso, demodulare il segnale PSK con il demodulatore differenziale asincrono, mostrato nella figura seguente, che opera direttamente a frequenza intermedia e non necessita di recupero di portante (deve però essere f0T = 2k
Nella stessa figura è riportato lo schema equivalente passa-basso riferito alla fIF di tale ricevitore. Il demodulatore differenziale effettua intrinsecamente la decodifica dei simboli di linea, fornendo direttamente i simboli di sorgente dk. Un sistema di trasmissione PSK con codifica differenziale e demodulatore differenziale asincrono è detto DPSK 13. Tale sistema fornisce una probabilità di errore pari a
La sensibilità del DPSK è migliore di 3 dB rispetto alla FSK ortogonale ed è esattamente peggiore di 3 dB rispetto al limite quantistico per OOK/DD. Inoltre, il peggioramento tra il ricevitore DPSK ed il ricevitore sincrono eterodina per PSK è limitato a circa 0.4 dB. La complessità del ricevitore DPSK è, infine, paragonabile a quella del ricevitore ASK o FSK a ramo singolo. Sfortunatamente il sistema DPSK risulta più fragile nei confronti delle inevitabili instabilità di fase/frequenza di oscillazione dei LASER di trasmissione e locale.
Un importante vantaggio dei ricevitori coerenti rispetto ai ricevitori a rivelazione diretta è la sensibilità del demodulatore; anche utilizzando metodi di modulazione e demodulazione, infatti, con prestazioni discoste dal limite quantistico, ad esempio 6.5 dB per una FSK con demodulatore asincrono, è possibile ottenere valori di sensibilità migliori per il ricevitore coerente, che non viene limitato dalla presenza di forte rumore termico e di fotorivelazione in eccesso fortemente limitativi per uno schema a rivelazione diretta. D'altro canto, nel progetto di un ricevitore coerente si devono considerare altri fattori di peggioramento delle prestazioni che sono assenti nel caso del semplice ricevitore DD.
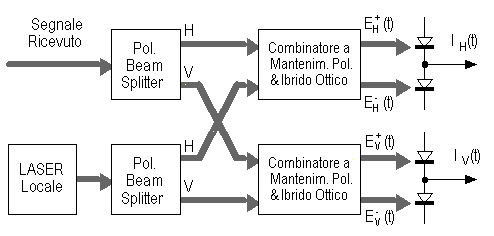
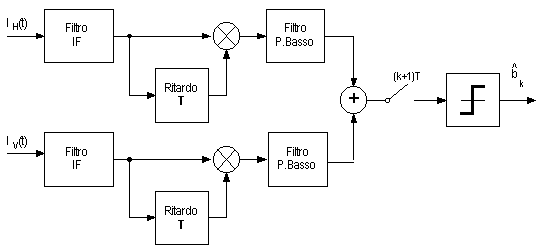
In esso sia il segnale ricevuto che il LASER locale vengono suddivisi da opportuni dispositivi (Polarization Beam Splitter) nelle rispettive componenti di polarizzazione orizzontale (H) e verticale (V), combinati e rivelati separatamente secondo una struttura in diversità bilanciata. I segnali elettrici IH e IV ottenuti vengono demodulati separatamente e ricombinati in banda base in modo da fornire un unico segnale utile alla stima dei dati, completamente indipendente dalla particolare SOP ricevuta. La combinazione dei segnali elettrici in banda base può avvenire, ad esempio, secondo lo schema del ricevitore DPSK in diversità di polarizzazione mostrato di seguito.
Il front-end del ricevitore in diversità di polarizzazione ha una complessità doppia rispetto a quello del ricevitore coerente bilanciato ma non necessita di dispositivi di tracciamento della SOP. Il raddoppio dei rami di rivelazione comporta una perdita limitata di sensibilità (meno di 0.4 dB per ciascuno dei asincroni analizzati).
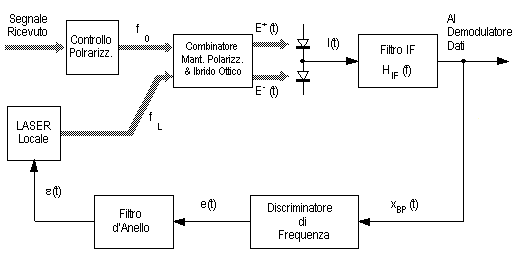
Sulla base dell'indicazione di un dispositivo discriminatore a frequenza intermedia, la corrente del LASER locale viene modificata in modo che la differenza tra la frequenza di emissione di esso e del LASER di trasmissione si mantenga pari alla fIF dello stadio elettrico. |

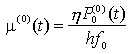 oppure
oppure 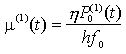
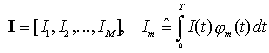 .
.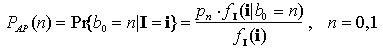
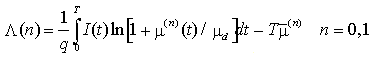
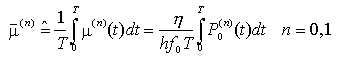 .
.
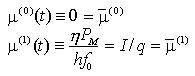
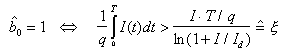 .
.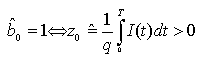 .
.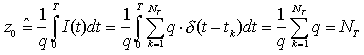
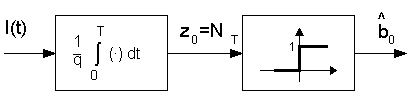
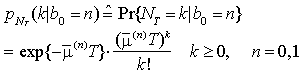 .
.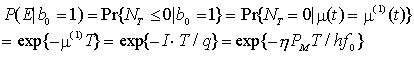
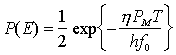 .
.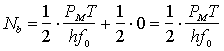
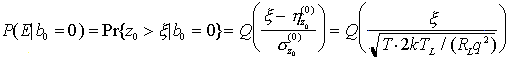
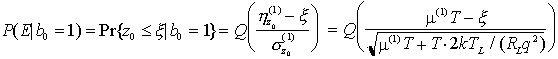
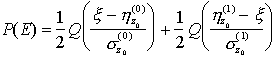 .
.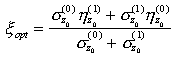 ;
;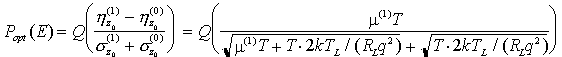
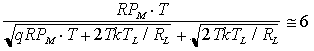 .
.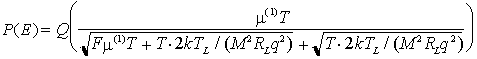
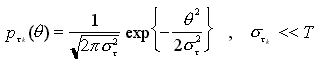
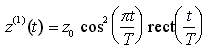
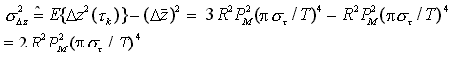 .
.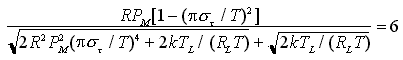
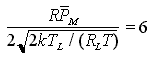
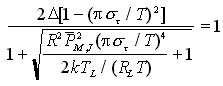 .
.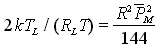
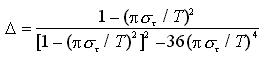 .
.
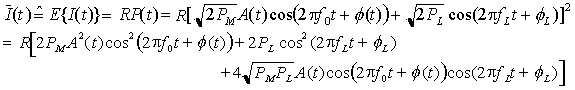 .
.
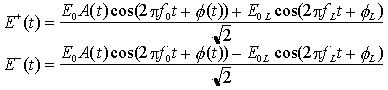
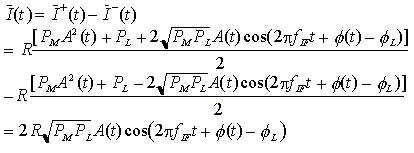

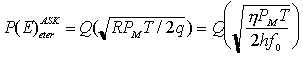 .
.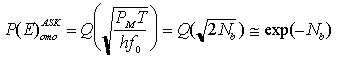 ,
,

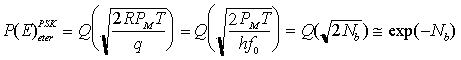
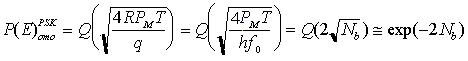
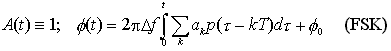
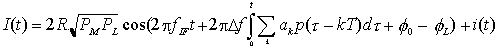 .
.