Sia I(t) un processo impulsi di Poisson filtrato di data intensità costante ![]() (processo omogeneo):
(processo omogeneo):
![]()
ove {tk} sono istanti di Poisson. Ci proponiamo dapprima di calcolare il valore medio statistico di tale processo
![]()
ove si è evidentemente già a conoscenza della stazionarietà in media del processo (ipotesi che comunque non verrà sfruttata nel seguito). Consideriamo adesso il processo IT(t) ottenuto applicando ad I(t) una finestra temporale di osservazione simmetrica di durata T
![]() .
.
Evidentemente I(t) coincide con il limite per T tendente ad infinito di IT(t), per cui, ipotizzando lecito il passaggio, ricaveremo I come limite per T tendente ad infinito di E{IT(t)}. Il numero N di impulsi di corrente il cui istante "di nascita" è compreso nell'intervallo di osservazione, cioè tra -T/2 e T/2, è una variabile aleatoria discreta che, per definizione di processo di Poisson, è distribuita secondo la legge Poissoniana con valor medio ![]() =
= ![]() *T
*T
![]() .
.
Supponiamo quindi di osservare nell'intervallo temporale (-T/2, T/2] esattamente n impulsi di corrente. Sotto tale condizione, gli n istanti di nascita tk, k = 1,...,n risultano v.a. indipendenti ed uniformemente distribuite nell'intervallo di osservazione,
![]() .
.
È semplice quindi calcolare il valor medio di IT(t) sotto questa condizione
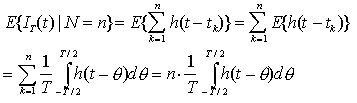 .
.
Per ricavare l'aspettazione incondizionata E{IT(t)} è necessario adesso effettuare una media ulteriore sul numero di impulsi N osservati nell'intervallo
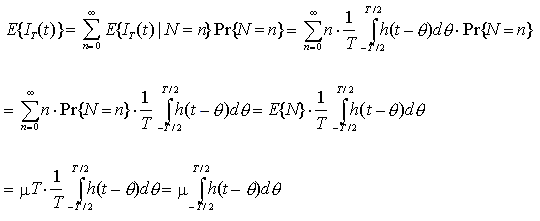 .
.
Facendo ora crescere illimitatamente T si arriva al risultato finale
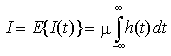 .
.
Poichè per il processo shot-noise di fotorivelazione l'integrale di h(t) è pari a q, si ha
![]() .
.
Simili calcoli riguardo alla funzione di autocorrelazione ![]() del processo IT(t) portano direttamente al risultato
del processo IT(t) portano direttamente al risultato
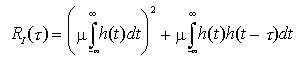
ovvero, considerando la funzione di autocovarianza di I(t), ![]() si ha
si ha
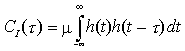
che corrisponde ad una d.s.p. Si(f) della componente a media nulla di disturbo i(t) = I(t) - I pari a
![]() .
.
A.2 - Calcolo della Funzione di Logverosimiglianza del Ricevitore IM/DD.
Il primo passo nel calcolo della funzione di logverosimiglianza ![]() (b0) è quello di determinare la densità di probabilità del vettore aleatorio I = [I1, I2, ..., IM] ottenuto espandendo la corrente di fotorivelazione I(t) su una base ortonormale. Scegliamo come base M-dimensionale di sviluppo quella in cui l'm-esimo elemento
(b0) è quello di determinare la densità di probabilità del vettore aleatorio I = [I1, I2, ..., IM] ottenuto espandendo la corrente di fotorivelazione I(t) su una base ortonormale. Scegliamo come base M-dimensionale di sviluppo quella in cui l'm-esimo elemento ![]() m è un impulso rettangolare diverso da zero sull'intervallo [(m-1)
m è un impulso rettangolare diverso da zero sull'intervallo [(m-1)![]() ,m
,m![]() ),
), ![]() = T/M, e, per normalizzazione, di ampiezza 1/(
= T/M, e, per normalizzazione, di ampiezza 1/(![]() )1/2. L'insieme di tali funzioni è schematicamente rappresentato nella figura seguente. Si ha quindi, nell'ipotesi di fotorivelatore a banda larga, cioè h(t) = q
)1/2. L'insieme di tali funzioni è schematicamente rappresentato nella figura seguente. Si ha quindi, nell'ipotesi di fotorivelatore a banda larga, cioè h(t) = q![]() (t),
(t),
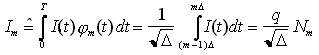
ove Nm è una v.a. di Poisson caratterizzata dalla seguente massa di probabilità condizionata al valore del simbolo b0
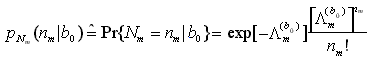
avendo definito
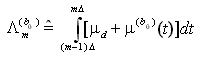
che è il parametro della m-esima v.a. di Poisson Nm, condizionato alla trasmissione del simbolo b0 e con una data corrente di buio Id = q*![]() d. Come si nota, le v.a. Nm sono proporzionali alle componenti Im del vettore aleatorio I, cosicché il problema della decisione ottima può essere risolto considerando in luogo di I il vettore aleatorio equivalente N = [N1, N2, ..., Nm].
d. Come si nota, le v.a. Nm sono proporzionali alle componenti Im del vettore aleatorio I, cosicché il problema della decisione ottima può essere risolto considerando in luogo di I il vettore aleatorio equivalente N = [N1, N2, ..., Nm].
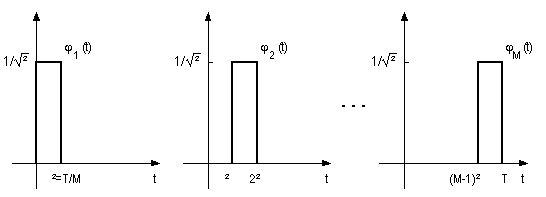
Fig. A.1 - Base ortonormale per la scomposizione della corrente I(t).
Le m v.a. Nm sono mutuamente indipendenti perchè ottenute da un processo impulsi di Poisson integrato su intervalli temporali disgiunti, e quindi la massa di probabilità del vettore aleatorio N = [N1, N2, ..., Nm] condizionata al simbolo trasmesso è data da
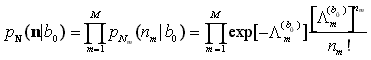
e la relativa funzione di logverosimiglianza ![]() M(b0) è data da
M(b0) è data da
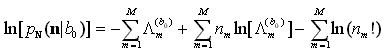 .
.
Consideriamo adesso i tre termini a secondo membro nella relazione precedente: il terzo termine può essere scartato perchè, non dipendendo da b0, non porta alcuna informazione utile ai fini della decisione (non interviene cioè nel problema di massimizzazione della funzione di logverosimiglianza rispetto al simbolo presunto). Il primo termine risulta
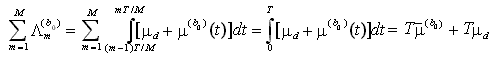
per cui, scartando ulteriormente il termine ininfluente T*![]() d, la funzione di logverosimiglianza equivalente è
d, la funzione di logverosimiglianza equivalente è
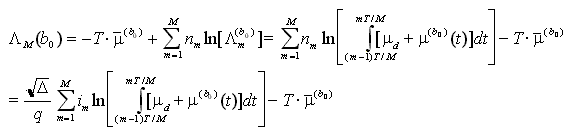
avendo tenuto conto che Im = q*Nm/(![]() )1/2. Resta dunque l'ultimo passo, e cioè quello di considerare una base completa, con
)1/2. Resta dunque l'ultimo passo, e cioè quello di considerare una base completa, con ![]() (e quindi
(e quindi ![]() tende a 0). In queste condizioni,
tende a 0). In queste condizioni,
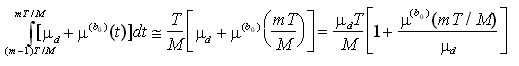
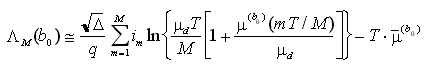
e quindi
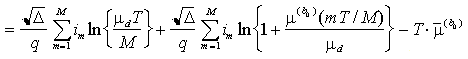
e, scartando ancora i termini non dipendenti da b0
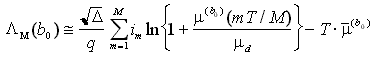
Riprendendo l'espressione di im, si nota anche che, quando ![]() ,
,
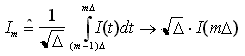
per cui
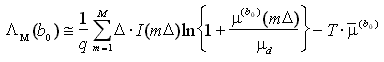
Infine, quando ![]() , la somma a secondo membro tende ad un integrale, portando al risultato
, la somma a secondo membro tende ad un integrale, portando al risultato
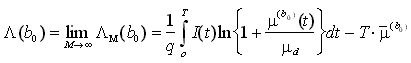
che rappresenta la forma della funzione di logverosimiglianza citata nel testo. Si noti infine che nei passaggi precedenti si è intenzionalmente scambiata la notazione del processo I(t) e le relative proiezioni aleatorie Im con la particolare realizzazione osservata i(t) avente componenti determinate im.
A.3 - Sincronizzazione del Clock.
Lo schema a blocchi di un ricevitore IM/DD che comprende il sincronizzatore di clock è mostrato di seguito.
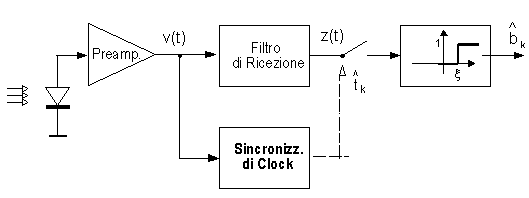
Fig. A.2 - Ricevitore IM/DD completo di recupero del sincronismo di clock.
Gli schemi di sincronizzazione di clock sono molteplici, e differenti sono, in generale, i loro principi di funzionamento. La principale difficoltà da risolvere nel progetto di questi schemi è, come già accennato, data dal fatto che lo spettro del segnale dati ricevuto non contiene alcuna componente periodica alla frequenza di clock 1/T sulla quale il ricevitore potrebbe facilmente sincronizzarsi. Una disposizione molto comune è quella mostrata nella figura seguente, che descrive la struttura di massima di un sincronizzatore, o rigeneratore, di clock a nonlinearità e filtro selettivo. Il segnale OOK v(t) all'ingresso del dispositivo viene ridotto a valor medio nullo e sagomato con un opportuno filtro. Il componente essenziale del circuito è poi il raddrizzatore a nonlinearità quadratica che rigenera una componente periodica alla frequenza di clock 1/T che non è presente originariamente nello spettro del segnale dati. Tale componente viene selezionata dal filtro passa-banda selettivo in modo da depurarla dai disturbi che la accompagnano e, opportunamente sfasata e squadrata per comodità d'uso, costituisce il riferimento di sincronismo del rigeneratore dati (campionatore e soglia) del ricevitore. La modalità di rigenerazione della componente periodica sulla quale il circuito seguente basa il proprio funzionamento è abbastanza semplice da comprendere.
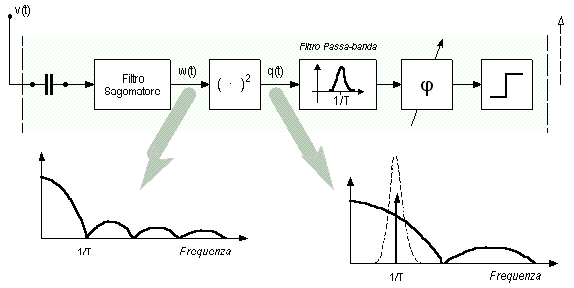
Fig. A.3 - Schema del sincronizzatore (rigeneratore) di clock a nonlinearità e filtro selettivo.
Consideriamo l'espressione del segnale dati w(t) a media nulla e sagomato, trascurando per semplicità il rumore shot e termico
![]()
ove p(t) è l'impulso elementare della modulazione OOK, e i simboli {ak} sono mutuamente indipendenti e (per effetto della riduzione a valor medio nullo) a valori equiprobabili {+1, -1}. Come la figura precedente suggerisce, tale segnale non contiene componenti periodiche. Il segnale q(t) all'uscita del quadratore (che in alcuni circuiti è sostituito da un semplice raddrizzatore) è quindi
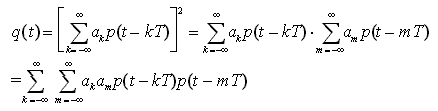
che può essere scomposto come segue: q(t) = s(t) + N(t), ove s(t) è una componente deterministica che vale
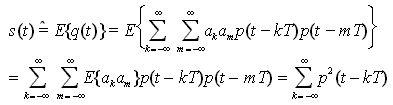
mentre N(t) è la componente di disturbo a valor medio nullo
![]()
detta rumore di pattern perchè dipendente dalla particolare successione (pattern) di simboli osservata. È chiaro che il segnale q(t) all'uscita della nonlinearità contiene una componente periodica a frequenza 1/T, data in particolare dalla componente a tale frequenza del segnale determinato periodico s(t) (si noti che tale componente ha ampiezza diversa da zero solo se la banda del segnale w(t) è maggiore della cosiddetta banda di Nyquist 1/2T). Questa componente viene selezionata dal filtro selettivo (insieme a una piccola parte del rumore di pattern) e costituisce il riferimento di sincronismo per la rigenerazione del segnale dati. Lo sfasatore variabile ha la funzione di compensare una volta per tutte in fase di calibrazione del circuito l'eventuale sfasamento che può intercorrere tra il riferimento ricostruito sulla base del segnale q(t) e l'istante di campionamento ottimo del segnale dati v(t).
A.4 - Potenza della Interazione ASE-ASE.
Il calcolo della potenza ![]() 2NN del termine di interazione ASE-ASE n2A(t) è semplice, considerando che l'ASE nA(t) può essere modellato come un processo Gaussiano bianco passa-banda, caratterizzato dalla d.s.p. SA(f) rappresentata di seguito.
2NN del termine di interazione ASE-ASE n2A(t) è semplice, considerando che l'ASE nA(t) può essere modellato come un processo Gaussiano bianco passa-banda, caratterizzato dalla d.s.p. SA(f) rappresentata di seguito.
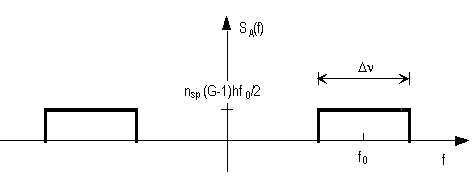
Fig. A.4 - Densità spettrale di potenza del rumore ASE.
La funzione di autocorrelazione di n2A(t) è allora
![]() .
.
Poichè, date le variabili aleatorie congiuntamente Gaussiane X, Y, Z, W, si ha
![]()
la R2(![]() ) diventa
) diventa
![]()
ove RA(![]() ) = E{nA(t)*nA(t-
) = E{nA(t)*nA(t-![]() )} è la funzione di autocorrelazione di nA(t). Dalla R2(
)} è la funzione di autocorrelazione di nA(t). Dalla R2(![]() ) si ricava immediatamente la d.s.p. S2(f) di n2A(t) come segue
) si ricava immediatamente la d.s.p. S2(f) di n2A(t) come segue
![]()
la cui componente in banda base (l'unica cui il fotorivelatore è sensibile) ha l'andamento delineato nella figura sottostante.
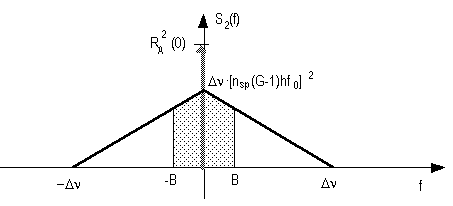
Fig. A.5 - Densità spettrale di potenza dell'interazione ASE-ASE.
Eliminando la componente continua R2A(0)*![]() (t), si ricava infine il contributo di potenza di rumore cercato come segue
(t), si ricava infine il contributo di potenza di rumore cercato come segue
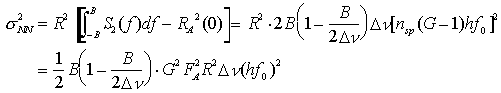 .
.