|
Rivelatori di
Segnali Ottici |
Introduzione
I fotorivelatori sono dispositivi che producono una corrente elettrica proporzionale all'intensità della radiazione luminosa che incide sull'area attiva dei medesimi. Il funzionamento dei rivelatori di segnali ottici si basa sul meccanismo di assorbimento della radiazione elettromagnetica da parte della materia, come descritto nel Cap. 2; nel seguito vedremo i due principali tipi di fotorivelatori: i fotodiodi p-i-n ed i fotodiodi valanga.
Ogni fotone incidente su di una porzione di semiconduttore intrinseco viene, teoricamente, assorbito producendo una coppia elettrone-lacuna nel materiale che, sotto l'azione di un campo elettrico esterno, contribuisce alla corrente di fotoconduzione. Ogni tipo di rivelatore fotoconduttivo richiede, per rivelare la presenza di radiazione luminosa, la presenza di una polarizzazione esterna ed, in particolare, in assenza di radiazione incidente la corrente nel circuito esterno è praticamente nulla dato il basso valore di conduttività del semiconduttore intrinseco. D'altra parte, in presenza di una radiazione incidente con potenza ottica utile P, il numero di portatori generati per assorbimento può essere rilevante e la corrente può assumere valori apprezzabili, provocando una cospicua caduta di tensione su di un resistore di polarizzazione collocato sul circuito esterno. Indicando con Iid la corrente prodotta per fotoconduzione in condizioni ideali di assorbimento totale ed assumendo che la radiazione luminosa abbia frequenza f0, si può scrivere che
 . .
Per un fotorivelatore reale la corrente misurata è minore del valore ideale di un fattore 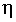 < 1 chiamato efficienza quantistica del dispositivo, per cui si ha < 1 chiamato efficienza quantistica del dispositivo, per cui si ha

ed, introducendo la responsivity del rivelatore di segnali ottici (misurata in A/W)

si ottiene la relazione che caratterizza fenomenologicamente il fotorivelatore
 . .
L'efficienza quantistica (o rendimento quantistico) può esprimersi in modo semplice tramite la relazione

ove RS è il coefficiente di riflettività dell'interfaccia aria/semiconduttore, 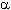 0 è il coefficiente di assorbimento per unità di lunghezza del materiale e d è la larghezza della zona di assorbimento. Ricordando le osservazioni fatte sull'emissione stimolata e sull'assorbimento [Cap. 2.2.3], sappiamo che il coefficiente di assorbimento 0 è il coefficiente di assorbimento per unità di lunghezza del materiale e d è la larghezza della zona di assorbimento. Ricordando le osservazioni fatte sull'emissione stimolata e sull'assorbimento [Cap. 2.2.3], sappiamo che il coefficiente di assorbimento 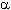 0, per un dato materiale, dipende fortemente dalla lunghezza d'onda 0, per un dato materiale, dipende fortemente dalla lunghezza d'onda  . Tale dipendenza è riportata nella figura seguente per alcuni materiali semiconduttori impiegati nella fabbricazione di fotorivelatori. . Tale dipendenza è riportata nella figura seguente per alcuni materiali semiconduttori impiegati nella fabbricazione di fotorivelatori.
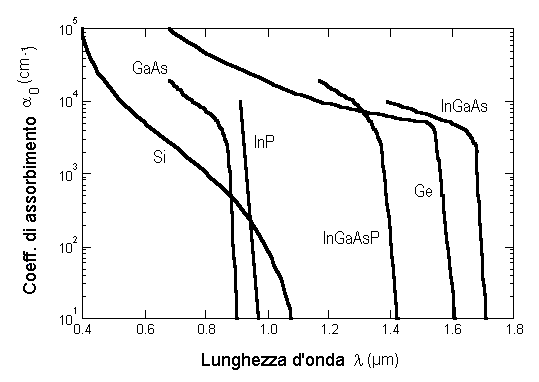
Fig. 3.1 - Coefficiente di assorbimento di vari semiconduttori intrinseci.
In figura si nota che esiste una lunghezza d'onda critica  c oltre la quale l'assorbimento è troppo piccolo per consentire l'uso del dispositivo come fotorivelatore. La c oltre la quale l'assorbimento è troppo piccolo per consentire l'uso del dispositivo come fotorivelatore. La  c è la lunghezza d'onda corrispondente all'energia minima necessaria al fotone incidente per essere assorbito (Eg = h*f0) provocando la transizione di un elettrone dalla banda di valenza alla banda di conduzione e, quindi, c è la lunghezza d'onda corrispondente all'energia minima necessaria al fotone incidente per essere assorbito (Eg = h*f0) provocando la transizione di un elettrone dalla banda di valenza alla banda di conduzione e, quindi,  c = h*c/Eg. c = h*c/Eg.

Fig. 3.2 - Assorbimento in un semiconduttore a gap indiretto.
Si noti che per quanto riguarda l'assorbimento non ha alcuna rilevanza la caratteristica di gap diretto o indiretto che è invece di fondamentale importanza per la realizzazione di buoni dispositivi emettitori a semiconduttore. Osservando la figura precedente, infatti, si nota che anche per un semiconduttore a gap indiretto si può avere facilmente una transizione diretta dalla banda di valenza a quella di conduzione perchè in quest'ultima esistono stati disponibili aventi stessa quantità di moto dello stato di partenza in banda di valenza.
3.1 - Il Diodo Fotorivelatore p-i-n
Un semiconduttore intrinseco può, dunque, servire da fotorivelatore ma tale materiale non può essere usato per applicazioni pratiche in quanto possiede una scarsa responsivity ed una forte inerzia elettrica.
Un fotorivelatore di tipo diverso si può realizzare facilmente dotando il semiconduttore di un campo elettrico intrinseco tale da provocare, in un circuito esterno, una corrente di fotoconduzione anche in assenza di polarizzazione esterna; tale tipo di dispositivo prende il nome di fotovoltaico. Una condizione del genere può essere realizzata mediante una giunzione p-n in cui, grazie al drogaggio di tipo opposto sui due lati, le coppie elettrone-lacuna generate per assorbimento di un fotone nella zona di svuotamento vengono allontanate dalla giunzione per effetto del campo elettrico interno creando la corrente di fotoconduzione. Nella pratica la giunzione viene polarizzata inversamente con un circuito esterno per aumentare il campo interno ed, in tal modo, i portatori generati per assorbimento vengono rimossi più velocemente dalla zona attiva. Ciò consente di mantenere la concentrazione dei portatori generati per assorbimento modesta nei rispettivi stati eccitati ed, allo stesso tempo, di massimizzare il tasso di assorbimento del materiale (RAS). Quando un fotone interagisce con la giunzione nella zona di svuotamento, la coppia elettrone-lacuna generata viene allontanata rapidamente dal campo esterno cosicché il movimento di portatori innescato (corrente di trascinamento) rinforza la debole corrente di conduzione inversa. Se, invece, la coppia elettrone-lacuna si trova al di fuori della zona attiva, per esempio nella zona p, la lacuna (portatore maggioritario) è libera di contribuire alla corrente di trascinamento immediatamente mentre l'elettrone (portatore minoritario) deve prima diffondere (corrente di diffusione) fino alla zona di svuotamento; analogamente nella zona n, fatte le debite modifiche. Questo meccanismo provoca una notevole inerzia elettrica, limitando la velocità di risposta e, quindi, la banda.
Un modo semplice per aumentare la banda del dispositivo consiste nell'interporre tra le due zone drogate (p ed n) una larga zona di semiconduttore intrinseco, creando il diodo p-i-n, come mostrato di seguito.

Fig. 3.3 - Diodo fotorivelatore p-i-n: (a) struttura di principio; (b) realizzazione ad eterostruttura in InGaAs.
Poiché lo strato centrale è intrinseco, esso rappresenta una zona di alta resistenza al passaggio della corrente creando, dunque, una forte caduta di tensione ai propri estremi; la zona di svuotamento si prolunga attraverso tutto lo strato intrinseco, che ha una lunghezza (fino a 50  m) maggiore di quella degli strati p ed n, cosicché l'assorbimento nella zona di diffusione può essere trascurato e la corrente di trascinamento è nettamente prevalente; il diodo p-i-n è, dunque, un dispositivo a larga banda (centinaia di MHz). Un incremento di banda si ottiene realizzando dispositivi con materiali ternari (InGaAs), in cui la zona di svuotamento può essere ridotta (meno di 10 m) maggiore di quella degli strati p ed n, cosicché l'assorbimento nella zona di diffusione può essere trascurato e la corrente di trascinamento è nettamente prevalente; il diodo p-i-n è, dunque, un dispositivo a larga banda (centinaia di MHz). Un incremento di banda si ottiene realizzando dispositivi con materiali ternari (InGaAs), in cui la zona di svuotamento può essere ridotta (meno di 10  m) minimizzando il tempo di attraversamento così da avere una banda da qualche GHz fino a oltre i 10 GHz. m) minimizzando il tempo di attraversamento così da avere una banda da qualche GHz fino a oltre i 10 GHz.
Per migliorare le prestazioni del fotorivelatore p-i-n si può utilizzare una eterostruttura in cui lo strato intrinseco è eterogeneo rispetto agli strati p ed n. Questa disposizione permette l'aumento del confinamento dell'assorbimento nella zona intrinseca alle frequenze di funzionamento: La Eg dello InGaAs ( 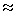 0.75 eV), per esempio, è tale da causare forte assorbimento nella banda 1.3 - 1.6 0.75 eV), per esempio, è tale da causare forte assorbimento nella banda 1.3 - 1.6  m mentre lo strato InP ha una Eg quasi doppia dello strato InGaAs ed è praticamente trasparente nella stessa banda, riducendo quasi a zero la componente diffusiva della fotocorrente. Poiché il dispositivo fotorivelatore è polarizzato inversamente, anche in completa assenza di potenza ottica incidente, nel circuito esterno scorre una piccola corrente di conduzione inversa Id, detta corrente di buio (Dark Current), di cui si deve tenere conto in fase di progetto di rivelatori per segnali ottici con fotorivelatori a semiconduttore. m mentre lo strato InP ha una Eg quasi doppia dello strato InGaAs ed è praticamente trasparente nella stessa banda, riducendo quasi a zero la componente diffusiva della fotocorrente. Poiché il dispositivo fotorivelatore è polarizzato inversamente, anche in completa assenza di potenza ottica incidente, nel circuito esterno scorre una piccola corrente di conduzione inversa Id, detta corrente di buio (Dark Current), di cui si deve tenere conto in fase di progetto di rivelatori per segnali ottici con fotorivelatori a semiconduttore.
3.2 - Il Diodo Fotorivelatore ad Effetto Valanga
Il problema principale dei diodi p-i-n è la scarsa responsivity, che resta dell'ordine del mA/mW, mentre per realizzare sistemi di trasmissione efficienti si ha interesse a sfruttare al massimo la potenza ottica trasmessa facendo incidere sul fotorivelatore ricevente la minima potenza prevista per avere le prestazioni richieste dal sistema. Tuttavia, in tali condizioni la corrente di fotorivelazione ottenuta dal diodo p-i-n è molto piccola e richiede una forte amplificazione elettrica. L'amplificazione elettrica di segnali così deboli, purtroppo, può indurre un peggioramento delle prestazioni dei ricevitori a causa del rumore introdotto nei primi stadi di amplificazione. Si preferisce, in molte applicazioni, utilizzare dispositivi che posseggono un guadagno intrinseco nell'azione di fotorivelazione stessa; questo significa che, questo tipo di dispositivi, producono più di una coppia di portatori per ogni fotone incidente sulla superficie attiva. Uno di questi dispositivi è il diodo valanga ( APD, Avalanche Photodiode) che, come dice il nome, si basa su di un effetto valanga provocato dal fenomeno della ionizzazione per impatto: un portatore all'interno del semiconduttore prodotto per assorbimento di un fotone viene accelerato dal forte campo elettrico presente nella zona attiva, dovuto alla forte polarizzazione inversa intenzionale; tale portatore può acquisire sufficiente energia cinetica per provocare la creazione di una ulteriore coppia elettrone-lacuna per ionizzazione di un atomo del reticolo invece che per assorbimento di un fotone. In pratica, l'elettrone in accelerazione cede energia ad un secondo elettrone nella banda di valenza che può passare nella banda di conduzione, e così via. Di fatto, un portatore "primario" generato per assorbimento di un fotone può generare un certo numero di coppie "secondarie" che contribuiscono alla fotoconduzione in uscita. APD, Avalanche Photodiode) che, come dice il nome, si basa su di un effetto valanga provocato dal fenomeno della ionizzazione per impatto: un portatore all'interno del semiconduttore prodotto per assorbimento di un fotone viene accelerato dal forte campo elettrico presente nella zona attiva, dovuto alla forte polarizzazione inversa intenzionale; tale portatore può acquisire sufficiente energia cinetica per provocare la creazione di una ulteriore coppia elettrone-lacuna per ionizzazione di un atomo del reticolo invece che per assorbimento di un fotone. In pratica, l'elettrone in accelerazione cede energia ad un secondo elettrone nella banda di valenza che può passare nella banda di conduzione, e così via. Di fatto, un portatore "primario" generato per assorbimento di un fotone può generare un certo numero di coppie "secondarie" che contribuiscono alla fotoconduzione in uscita.
L'attitudine di un semiconduttore alla ionizzazione viene quantificata dai coefficienti di ionizzazione 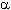 h (per le lacune) e h (per le lacune) e 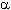 e (per gli elettroni), che rappresentano il numero medio di ionizzazioni che si verificano nel materiale per unità di lunghezza (cm), per un fissato valore del campo elettrico esterno che provoca l'accelerazione. e (per gli elettroni), che rappresentano il numero medio di ionizzazioni che si verificano nel materiale per unità di lunghezza (cm), per un fissato valore del campo elettrico esterno che provoca l'accelerazione.
A partire da un diodo p-i-n un fotorivelatore APD è realizzato aggiungendo uno strato di semiconduttore p, detto regione di moltiplicazione, come mostrato di seguito.

Fig. 3.4 - Schema di principio (a) e realizzazione (b) di un rivelatore APD SAM con eterogiunzione.
Nella regione di moltiplicazione ha sede il processo valanga mentre lo strato i ha ancora la funzione di generazione degli elettroni primari. Questo tipo di fotorivelatori è indicato come SAM APD (Separate Absorption and Multiplication APD).
Analizziamo in dettaglio l'effetto moltiplicativo facendo riferimento alla figura precedente, prendendo un sistema di riferimento, come indicato, con l'asse delle ascisse ortogonale alla giunzione ed assumendo come origine l'interfaccia i-p. Indichiamo con Je(x) e Jh(x) rispettivamente le densità di corrente di elettroni e lacune all'interno della zona di moltiplicazione; la somma delle due densità deve essere costante in tutta la zona di guadagno, per mantenere la neutralità della carica a regime. Supponendo che si abbia assorbimento nella sola zona i per x = d si possono trascurare le lacune iniettate dalla zona n, ovvero porre Jh(d) = 0. La densità di corrente per x = d dovrà perciò essere pari alla sola Je(d)

e, inoltre, nel punto generico x l'incremento della densità di corrente di elettroni per effetto valanga è pari a

ove l'incremento comprende due termini dovuti ai due tipi di portatori 9 ionizzati. Dalle due relazioni precedenti si ricava la semplice equazione differenziale

dalla quale si ricava, per ogni valore della densità di elettroni "primari" iniettata Je(0), l'espressione del fattore di moltiplicazione (guadagno) dello APD

ove kA è il rapporto di ionizzazione. È evidente che per d = 0 si ha M = 1, in quanto il dispositivo non presenta nessuna zona di moltiplicazione mentre per  si ha si ha  , cioè il dispositivo presenta un effetto di breakdown distruttivo. , cioè il dispositivo presenta un effetto di breakdown distruttivo.
Dalla descrizione precedente è chiaro che la relazione fenomenologica che lega la potenza ottica incidente alla corrente prodotta si modifica come segue

e, quindi, possiamo pensare che la responsivity dello APD sia pari a
 . .
Per buoni fotorivelatori APD al Si si ha che M varia, tipicamente, dalla decina al centinaio con un guadagno corrispondente di 10 - 20 dB.
Il guadagno che si ottiene negli APD si paga in termini di rumore in quanto il processo di moltiplicazione dei portatori che contribuiscono alla corrente di uscita è intrinsecamente "rumoroso". Ciò è dovuto al fatto che il coefficiente che fornisce il numero di elettroni nella corrente di uscita provocati da un unico fotone assorbito nella zona i non è una costante ma è una variabile aleatoria, per la natura quantistica dei fenomeni stessi, che assume valori diversi nei diversi eventi di assorbimento e moltiplicazione. Il guadagno M può considerarsi una costante solo facendo riferimento ad opportune "medie" della corrente. Il valore istantaneo di I, in uscita allo APD, è inevitabilmente accompagnato da una componente aleatoria di disturbo in eccesso che non è presente nella corrente generata nei diodi p-i-n. Analizzando il fenomeno si trova che, al fine di minimizzare il rumore intrinseco di moltiplicazione, per minimizzare la varianza di M lo APD deve avere KA << 1 oppure kA >> 1, cioè il meccanismo di moltiplicazione deve essere affidato ad un solo tipo di portatori di carica.
Nonostante questo inconveniente i rivelatori APD vengono largamente usati nei sistemi per telecomunicazioni in quanto semplificano notevolmente il progetto della parte frontale elettrica del ricevitore che, adesso, non necessita dell'amplificazione spinta richiesta per i diodi p-i-n. È necessario, tuttavia, tenere presente che maggiore è il guadagno M offerto dallo APD, minore risulta la banda elettrica del dispositivo poiché aumenta il tempo necessario alla generazione dei portatori secondari per effetto valanga e, quindi, il tempo necessario alla loro rimozione dalla zona di moltiplicazione verso il circuito esterno. La dipendenza risulta una quasi esatta inversa proporzionalità, cosicché può dirsi che il prodotto guadagno-banda per una certa tecnologia di fabbricazione è una costante. Per trasmissioni in I finestra vengono utilizzati diodi valanga al Si che presentano bassa rumorosità ed alto guadagno in quanto per il Si kA 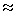 0.02; la fabbricazione di buoni APD per sistemi operanti in II e III finestra presenta alcune difficoltà poiché, per i materiali più adatti in tale range, si ha kA 0.02; la fabbricazione di buoni APD per sistemi operanti in II e III finestra presenta alcune difficoltà poiché, per i materiali più adatti in tale range, si ha kA 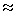 1 che comporta rumorosità dello APD stesso come descritto sopra. Questo problema viene risolto con una eterostruttura in cui lo strato di guadagno è costituito da InP, che ha 1 che comporta rumorosità dello APD stesso come descritto sopra. Questo problema viene risolto con una eterostruttura in cui lo strato di guadagno è costituito da InP, che ha 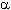 h > h > 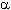 e, e sopporta alti valori di campo elettrico esterno senza fenomeni di breakdown. Nella eterostruttura SAM si nasconde, tuttavia, un inconveniente dovuto alla differenza tra la Eg di InP e la Eg di InGaAs piuttosto ampia; questo porta ad un intrappolamento delle lacune all'interfaccia della eterogiunzione con un sensibile aumento del tempo di transito verso la zona di guadagno e, quindi, diminuzione del tempo di risposta del dispositivo. Il problema viene risolto aggiungendo un ulteriore strato di materiale quaternario (InGaAsP) con una Eg intermedia ed ottenendo il SAGM (Separate Absoption, Grading and Multiplication), mostrato di seguito. Per questi dispositivi il prodotto guadagno-banda è di qualche GHz. e, e sopporta alti valori di campo elettrico esterno senza fenomeni di breakdown. Nella eterostruttura SAM si nasconde, tuttavia, un inconveniente dovuto alla differenza tra la Eg di InP e la Eg di InGaAs piuttosto ampia; questo porta ad un intrappolamento delle lacune all'interfaccia della eterogiunzione con un sensibile aumento del tempo di transito verso la zona di guadagno e, quindi, diminuzione del tempo di risposta del dispositivo. Il problema viene risolto aggiungendo un ulteriore strato di materiale quaternario (InGaAsP) con una Eg intermedia ed ottenendo il SAGM (Separate Absoption, Grading and Multiplication), mostrato di seguito. Per questi dispositivi il prodotto guadagno-banda è di qualche GHz.

Fig. 3.5 - Struttura di un APD ad eterostruttura SAGM.
3.3 - Caratterizzazione Matematica dei Fotorivelatori
3.3.1 - Fotodiodo p-i-n
Abbiamo visto brevemente le caratteristiche fisiche e funzionali dei principali dispositivi fotorivelatori. Vediamo adesso una caratterizzazione matematica del comportamento di essi necessaria nella fase di progetto e di valutazione delle prestazioni (BER o SNR) per i vari sistemi di trasmissione.
Consideriamo un diodo p-i-n investito da una radiazione luminosa avente vettore di Poiynting costante nel tempo P0 (potenza ottica utile). Ciò equivale a considerare in prima approssimazione la corrente di uscita costante e pari ad I = RP0 ma, in realtà, per effetto della aleatorietà del fenomeno di assorbimento essa sarà composta da una molteplicità di contributi elementari, ognuno dovuto al passaggio di un elettrone nel circuito di uscita, prodotto per assorbimento di un fotone incidente
 , ,
ove h(t) rappresenta l'impulso di corrente elementare provocato da un singolo elettrone 10; con tk si è indicato l'istante aleatorio di comparsa del k-esimo elettrone nel circuito di uscita. Si può dimostrare che gli istanti {tk} sono istanti di Poisson e che, quindi, I(t) rappresenta, dal punto di vista statistico, un processo impulsi di Poisson omogeneo filtrato. Nella figura seguente è rappresentato, simbolicamente, una possibile realizzazione del processo I(t) ed una sua interpretazione. La corrente di fotorivelazione può essere vista come il risultato di una operazione di "filtraggio", con un filtro avente risposta impulsiva h(t), di un processo impulsi di Poisson 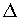 (t) in cui, in corrispondenza dell'assorbimento del k-esimo fotone all'istante tk si ha la generazione di una funzione impulsiva. (t) in cui, in corrispondenza dell'assorbimento del k-esimo fotone all'istante tk si ha la generazione di una funzione impulsiva.

Fig. 3.6 - Processo impulsi di Poisson filtrato.
Si può identificare, in questo senso, h(t) come una sorta di "risposta impulsiva equivalente" del fotorivelatore determinata, in ultima analisi, dalle caratteristiche elettriche del dispositivo. Il numero medio (intensità  ) di impulsi elementari di corrente nell'unità di tempo risulta legato alla potenza ottica incidente sul fotorivelatore. Per derivare il legame tra ) di impulsi elementari di corrente nell'unità di tempo risulta legato alla potenza ottica incidente sul fotorivelatore. Per derivare il legame tra  e P0 osserviamo che il valore medio della corrente di uscita è stato espresso, fenomenologicamente, come I = RP0; d'altronde il teorema di Campbell A (dalla teoria dei processi di Poisson) stabilisce che e P0 osserviamo che il valore medio della corrente di uscita è stato espresso, fenomenologicamente, come I = RP0; d'altronde il teorema di Campbell A (dalla teoria dei processi di Poisson) stabilisce che
 , ,
da cui si ottiene che
 . .
L'intensità  del processo è costante (processo omogeneo) ed, in particolare, ciò comporta che il numero N di impulsi di corrente originati in un qualunque intervallo temporale di ampiezza T è una variabile aleatoria descritta di Poisson con parametro del processo è costante (processo omogeneo) ed, in particolare, ciò comporta che il numero N di impulsi di corrente originati in un qualunque intervallo temporale di ampiezza T è una variabile aleatoria descritta di Poisson con parametro 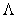 = =  T. È possibile, allora, scrivere la corrente di uscita dal fotorivelatore come T. È possibile, allora, scrivere la corrente di uscita dal fotorivelatore come

ove i(t) è un processo di disturbo a valore medio nullo detto shot noise o rumore di granularità. Dal teorema di Campbell si trova, inoltre, che i(t) è un processo stazionario in senso lato e ha densità spettrale di potenza (d.s.p.)

ove H(f) è la trasformata di Fourier di h(t).
Nella figura seguente è rappresentata la situazione in cui la banda B del ricevitore che segue il fotorivelatore è molto minore della banda intrinseca del fotorivelatore stesso Bf , quest'ultimo determinato da H(f).

Fig. 3.7 - Densità spettrale di potenza del rumore shot.
Ai fini del calcolo della potenza di rumore shot in ingresso al ricevitore si può approssimare la relazione precedente con una d.s.p. costante

e, quindi, il disturbo i(t) può considerarsi bianco con tale densità spettrale di potenza. Questa relazione mostra chiaramente come la densità spettrale di potenza del disturbo sia dipendente dal livello del segnale utile: maggiore è P0, maggiore è il valore medio I di uscita e maggiore risulta anche la Si(f)
 . .
Nell'ipotesi Bf >> B si può definire un rapporto segnale-rumore intrinseco del fotorivelatore
 . .
Da esso si vede che quando SNRpin >> 1, ovvero quando  >> B, la potenza ottica che viene rivelata è cospicua, in quanto l'energia viene raccolta nell'ambito di intervalli temporali aventi un'ampiezza paragonabile alla costante di tempo intrinseca del ricevitore 1/B. Una proprietà dei processi di Poisson derivante dal teorema del limite centrale assicura, in questo caso, che le statistiche di I(t) possono essere considerate con ottima approssimazione, coincidenti con quelle di un processo Gaussiano avente media e densità spettrale di potenza pari a quelle di I(t) stesso. >> B, la potenza ottica che viene rivelata è cospicua, in quanto l'energia viene raccolta nell'ambito di intervalli temporali aventi un'ampiezza paragonabile alla costante di tempo intrinseca del ricevitore 1/B. Una proprietà dei processi di Poisson derivante dal teorema del limite centrale assicura, in questo caso, che le statistiche di I(t) possono essere considerate con ottima approssimazione, coincidenti con quelle di un processo Gaussiano avente media e densità spettrale di potenza pari a quelle di I(t) stesso.
3.3.2 - Fotodiodo Valanga
Nel caso di un rivelatore valanga, su cui incide lo stesso flusso costante di radiazione luminosa, la corrente in uscita è modellata mediamente la seguente relazione

ove {Mk} è una successione di variabili aleatorie supposte indipendenti a valori interi equidistribuite che rappresentano, ciascuna, il numero aleatorio di elettroni generati per effetto valanga nel k-esimo evento di assorbimento all'istante tk. La corrente di uscita è, in questo caso, un processo impulsi di Poisson marcato, ovvero pesato dai coefficienti {Mk} statisticamente indipendenti dagli istanti {tk}, si trova che

e, poiché, dal punto di vista fenomenologico si ha

si ottiene immediatamente la relazione
 . .
Poiché  misura la cadenza di assorbimento dei fotoni a prescindere dal fenomeno di moltiplicazione, esso assume ancora l'espressione misura la cadenza di assorbimento dei fotoni a prescindere dal fenomeno di moltiplicazione, esso assume ancora l'espressione

ed M assume, quindi, il significato di guadagno medio di fotorivelazione. Utilizzando ancora il teorema di Campbell nell'ipotesi che i guadagni {Mk} siano mutuamente indipendenti, si trova che il disturbo a valore medio nullo prodotto da un fotodiodo valanga

sovrapposto alla componente utile costante della corrente ha densità spettrale di potenza pari a
 , ,
da cui si possono fare considerazioni simili a quelle fatte nel caso del fotorivelatore p-i-n. Dalla relazione precedente si nota che, per effetto della aleatorietà del fenomeno di moltiplicazione, la rumorosità dello APD è incrementata rispetto a quella ipotetica ( ) competente ad un fotorivelatore in cui il guadagno M fosse costante su ogni fotone assorbito. Il fattore di incremento è pari a ) competente ad un fotorivelatore in cui il guadagno M fosse costante su ogni fotone assorbito. Il fattore di incremento è pari a

che viene chiamato fattore di rumore in eccesso del diodo valanga. Infatti, dal calcolo del rapporto segnale-rumore intrinseco dello APD, nell'ipotesi Bf >> B, si ottiene

da cui è evidente un incremento intrinseco di rumorosità rispetto al diodo p-i-n proprio di tale fattore.
Mediante un'analisi dei fenomeni connessi alla ionizzazione per impatto si ricava una espressione del fattore F, in dipendenza di k = min(kA, 1/kA), il cui andamento è riportato nella figura seguente


Fig. 3.8 - Fattore di rumore di un rivelatore APD.
Risulta chiara la necessità di realizzare rivelatori valanga con kA molto piccolo (ionizzazione per soli elettroni) o molto grande (ionizzazione per sole lacune) in quanto in entrambe queste condizioni k << 1 e F 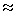 2 con un peggioramento di soli 3 dB dello SNRAPD rispetto allo SNRpin. Nonostante il peggioramento dello SNRAPD intrinseco, vedremo più avanti il miglioramento dello SNR globale del ricevitore ottenuto mediante l'uso di rivelatori APD anzichè rivelatori p-i-n. 2 con un peggioramento di soli 3 dB dello SNRAPD rispetto allo SNRpin. Nonostante il peggioramento dello SNRAPD intrinseco, vedremo più avanti il miglioramento dello SNR globale del ricevitore ottenuto mediante l'uso di rivelatori APD anzichè rivelatori p-i-n.
3.3.3 - Potenza Ottica Variabile nel Tempo
Nell'analisi del rumore di fotorivelazione effettuata si è prevista una potenza ottica incidente costante P0. Quando si ha che fare con segnali modulati tale grandezza varia nel tempo, cioè P0 = P0(t). La corrente di uscita del fotorivelatore è, in questo caso, ancora un processo di Poisson filtrato detto non omogeneo (o non stazionario) perchè l'intensità di tale processo non è costante nel tempo ma dipende dalla potenza ottica incidente. La dipendenza è simile a quella già ottenuta nel caso di radiazione costante ed è fornita dalla relazione
 . .
Il processo I(t) non è stazionario e, quindi, in questo caso le statistiche del numero Nt di impulsi di corrente nell'intervallo temporale (t, t + T] dipendono dall'ampiezza dell'intervallo T e, anche, dal valore particolare di t scelto. Questo perchè Nt è una variabile aleatoria di Poisson con parametro

e, condizionatamente all'osservare esattamente n eventi nell'intervallo su citato (cioè condizionatamente ad Nt = n), i relativi istanti t1 , ...., tn pur essendo ancora indipendenti ed equidistribuiti come nel caso del processo omogeneo, hanno una densità di probabilità non uniforme
 . .
Combinando queste proprietà si dimostra che il valore medio di I(t) è pari a
 . .
Se il segnale trasmesso modula direttamente la potenza ottica trasmessa in fibra, l'intensità  (t) del processo di uscita al fotorivelatore è proporzionale a tale segnale; le relazioni precedenti evidenziano, allora, la particolarità del canale di trasmissione ottico a modulazione di intensità e rivelazione diretta (maggiormente dettagliato più avanti) che è quella di filtrare il segnale modulato con la risposta impulsiva del fotorivelatore h(t). Ammettendo che la banda B del segnale ottico modulato sia molto minore della banda del fotorivelatore (Bf >> B), il valore medio della corrente di uscita ricalca senza distorsioni la modulazione impressa sul segnale ottico; in ogni caso, anche quando B (t) del processo di uscita al fotorivelatore è proporzionale a tale segnale; le relazioni precedenti evidenziano, allora, la particolarità del canale di trasmissione ottico a modulazione di intensità e rivelazione diretta (maggiormente dettagliato più avanti) che è quella di filtrare il segnale modulato con la risposta impulsiva del fotorivelatore h(t). Ammettendo che la banda B del segnale ottico modulato sia molto minore della banda del fotorivelatore (Bf >> B), il valore medio della corrente di uscita ricalca senza distorsioni la modulazione impressa sul segnale ottico; in ogni caso, anche quando B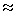 Bf , la variazione di P0(t) può essere recuperata con facilità, ad esempio usando un filtro equalizzatore elettrico nel ricevitore che compensi opportunamente le distorsioni introdotte dalla risposta non ideale h(t) del fotorivelatore. Bf , la variazione di P0(t) può essere recuperata con facilità, ad esempio usando un filtro equalizzatore elettrico nel ricevitore che compensi opportunamente le distorsioni introdotte dalla risposta non ideale h(t) del fotorivelatore.
Poiché la componente di disturbo a media nulla non è stazionaria, la densità spettrale di potenza può essere calcolata con alcune accortezze. Definendo una autocorrelazione mediata

si trova una densità spettrale di potenza media del disturbo pari a
 . .
Noto, allora, l'andamento di P0(t) è possibile svolgere calcoli di rapporto segnale-rumore (mediato nel tempo) per il ricevitore che segue il fotorivelatore. Nel caso Bf >> B il rapporto segnale-rumore medio per un diodo p-i-n sarà pari, ad esempio, a
 . .
3.4 - Calcolo dello SNR dei Ricevitori per Segnali Ottici
La modellizzazione matematica precedente permette una valutazione delle prestazioni dei vari tipi di ricevitori per segnali ottici modulati che utilizzano questi dispositivi. Un tale tipo di studio, naturalmente, deve essere effettuato in modo circostanziato a seconda del tipo di trasmissione e del tipo di modulazione. Una caratterizzazione efficace anche se rozza, tuttavia, può essere effettuata indipendentemente dal tipo di segnale modulato effettivamente usato se, come parametro di bontà, si usa il rapporto segnale-rumore nella parte frontale elettrica ( front-end) del ricevitore. front-end) del ricevitore.
Il front-end del ricevitore può considerarsi, in prima approssimazione, dipendente dalla sola banda del segnale modulante che deve essere rivelato. A tal fine l'unica grandezza necessaria al calcolo del rapporto segnale-rumore è la banda equivalente di rumore B del ricevitore, commisurata alla banda del segnale da rivelare, che prescinde da specificazioni ulteriori sulla natura del segnale stesso.
3.4.1 - Calcolo dello SNR per il Ricevitore con Diodo p-i-n
Consideriamo, allora, lo schema a blocchi di una possibile realizzazione di un ricevitore per segnali ottici modulati, mostrato di seguito.

Fig. 3.9 - Struttura di principio della parte frontale dei ricevitori per segnali ottici.
Il fotorivelatore è chiuso su di un resistore di carico RL, in modo che la relativa caduta di tensione provocata dalla corrente I(t) di fotorivelazione sia amplificata dall'amplificatore di tensione successivo, avente guadagno G. Tale amplificatore presenta una impedenza di ingresso elevata, in particolare, molto maggiore di RL; questa configurazione, infatti, viene detta ad alta impedenza. Per semplicità l'analisi viene svolta per un segnale non modulato in quanto il caso di un segnale modulato non comporta differenze concettuali e conduce a risultati analoghi al caso preso in considerazione nel seguito. Abbiamo visto che la componente utile I uscente dal fotorivelatore, p-i-n in questo caso, è accompagnata da una d.s.p. pari a q*I; se B è la banda equivalente di rumore del ricevitore il contributo di rumore shot equivale ad una potenza di rumore all'ingresso dell'amplificatore pari a
 . .
Nel caso in cui la potenza ottica rivelata è piccola e, quindi, è piccola I, si deve considerare anche la corrente di buio Id fino ad ora trascurata. Poiché anche la Id è caratterizzabile come un processo impulsi di Poisson filtrato (dalla h(t)), il valore medio di esso è proprio la Id mentre la componente di fluttuazione aleatoria a valore medio nullo ha d.s.p. pari a q*Id. La corrente di bui genera, quindi, un disturbo la cui potenza è pari a
 . .
Il resistore RL introduce, inoltre, una componente di disturbo, dovuta al rumore termico la cui d.s.p. è, se la temperatura del resistore è TL, pari a 2kTL/RL, ove k è la costante di Boltzmann. La potenza associata al rumore termico è dunque
 . .
Se è nota, inoltre, la cifra di rumore FA dell'amplificatore riferita alla temperatura TL, il rumore totale, inteso come somma del rumore termico di RL e di quello interno dell'amplificatore riportato all'ingresso dello stesso, è pari a
 . .
Osservando che tutte le componenti di disturbo prese in considerazione fino ad ora possono ritenersi indipendenti, il rapporto segnale-rumore all'uscita dell'amplificatore è pari a
 . .
Considerando i valori tipici di P0 ed R per il diodo p-i-n si osserva che 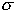 2Tot tende a dominare nettamente i contributi di rumore dovuti alla fotorivelazione ed alla corrente di buio, cosicché le prestazioni del ricevitore sono sostanzialmente determinate dalla RL di carico del fotorivelatore. 2Tot tende a dominare nettamente i contributi di rumore dovuti alla fotorivelazione ed alla corrente di buio, cosicché le prestazioni del ricevitore sono sostanzialmente determinate dalla RL di carico del fotorivelatore.
3.4.2 - Regime Limitato dal Rumore Termico e Regime Limitato dal Rumore di Fotorivelazione
Nel caso in cui 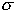 2Tot >> 2Tot >> 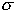 2D, 2D, 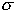 2SH si dice che il ricevitore si trova in regime di limitazione per rumore termico. In queste condizioni le componenti di rumore shot e di corrente di buio possono essere trascurate ed il rapporto segnale-rumore diviene 2SH si dice che il ricevitore si trova in regime di limitazione per rumore termico. In queste condizioni le componenti di rumore shot e di corrente di buio possono essere trascurate ed il rapporto segnale-rumore diviene
 . .
Il disturbo è, in tal caso, additivo gaussiano bianco indipendente dal segnale cosicché, qualunque sia il tipo di modulazione, è semplice valutare le prestazioni dei ricevitori per le differenti tecniche di trasmissione. Dalla relazione precedente si nota che le prestazioni del ricevitore migliorano scegliendo una RL più grande possibile. Sfortunatamente l'esigenza di minimizzare la rumorosità del ricevitore è in conflitto con la necessità di mantenere una banda elevata. Consideriamo, infatti, la presenza della capacità CL all'ingresso dell'amplificatore, derivante dal parallelo della capacità d'ingresso dell'amplificatore e di quella intrinseca del fotorivelatore, è chiaro che il limite di banda fT del ricevitore è fT = 1/(2 RLCL). Ogni incremento della RL porta, inevitabilmente, ad una riduzione della banda del ricevitore per cui, in generale, è necessario trovare un valore di compromesso. Si adotta, talvolta, uno schema di ricevitore con amplificatore a bassa impedenza d'ingresso Ri, nel caso in cui l'esigenza di una larga banda predomina su quella di basso rumore, cosicché la resistenza da considerare diviene, in pratica, il parallelo di RL e della Ri stessa. RLCL). Ogni incremento della RL porta, inevitabilmente, ad una riduzione della banda del ricevitore per cui, in generale, è necessario trovare un valore di compromesso. Si adotta, talvolta, uno schema di ricevitore con amplificatore a bassa impedenza d'ingresso Ri, nel caso in cui l'esigenza di una larga banda predomina su quella di basso rumore, cosicché la resistenza da considerare diviene, in pratica, il parallelo di RL e della Ri stessa.
Un diverso approccio per evitare limitazioni in banda consiste nell'uso di un front-end a transimpedenza, in cui l'amplificatore di tensione in parallelo alla RL viene sostituito con l'amplificatore di corrente mostrato di seguito.

Fig. 3.10 - Parte frontale dei ricevitori per segnali ottici.
In questo caso l'impedenza di ingresso dell'amplificatore di tensione reazionato in corrente dalla Rf è pari a Ri = Rf/G, che può assumere un valore piuttosto basso (G >> 1). La resistenza vista dalla capacitá CL è il parallelo di RL con Ri, sostanzialmente pari in questo caso ad Ri e la banda del ricevitore è, quindi, fT = 1/(2 CLRi) che risulta in generale maggiore del valore relativo al front-end ad alta impedenza. La corrente di fotorivelazione viene derivata verso l'amplificatore (in pratica scorre in Rf) e viene amplificata e trasformata nella tensione Vout = -Rf*I all'uscita dell'amplificatore. La corrente di rumore generata dal resistore Rf, avente d.s.p. pari a 2kTf/Rf, viene semplicemente a sommarsi a quella generata dal resistore; entrambe queste componenti possono adesso essere ridotte aumentando i valori delle resistenze senza penalizzare eccessivamente la banda passante. CLRi) che risulta in generale maggiore del valore relativo al front-end ad alta impedenza. La corrente di fotorivelazione viene derivata verso l'amplificatore (in pratica scorre in Rf) e viene amplificata e trasformata nella tensione Vout = -Rf*I all'uscita dell'amplificatore. La corrente di rumore generata dal resistore Rf, avente d.s.p. pari a 2kTf/Rf, viene semplicemente a sommarsi a quella generata dal resistore; entrambe queste componenti possono adesso essere ridotte aumentando i valori delle resistenze senza penalizzare eccessivamente la banda passante.
Le descrizioni fatte fino ad ora sono di principio e devono essere raffinate nella reale progettazione del front-end. Si deve, ad esempio, tenere conto che nel ricevitore a transimpedenza può rivelarsi importante la capacità parassita Cf del resistore di reazione, fin qui non considerato, che può portare ad una prematura limitazione in banda per effetto Miller. Alcuni fotorivelatori vengono comunque commercializzati con uno stadio front-end di preamplificazione elettrica interno al package (generalmente realizzato in configurazione a transimpedenza) con dati dichiarati di banda e corrente totale equivalente di rumore, che semplifica notevolmente l'uso del componente nel progetto globale del ricevitore.
Se la progettazione del front-end è corretta, in modo da ridurre adeguatamente il rumore termico, e la potenza ottica rivelata è sufficientemente elevata, si dice che il ricevitore e nel regime limitato dal rumore di fotorivelazione (shot-noise limited). In queste condizioni, generalmente, il rumore dovuto alla corrente di buio è trascurabile rispetto al rumore shot e il rapporto segnale-rumore è quello intrinseco del fotorivelatore
 . .
3.4.3 - Calcolo dello SNR per il Ricevitore con Diodo Valanga
Il calcolo del rapporto segnale-rumore per un ricevitore con diodo valanga (APD) può essere svolto nello stesso modo visto per il ricevitore con diodo p-i-n da cui, viste le condizioni generali sulle possibili strutture del front-end, si ottiene

ove I ed Id sono, rispettivamente, le correnti medie utile e di buio relative ai soli portatori primari, cioè le componenti che si avrebbero in assenza di guadagno dello APD. In condizioni di regime dominato dal rumore termico si ha

che evidenzia un guadagno di un fattore M2 rispetto al rapporto segnale-rumore del ricevitore con un diodo p-i-n, interamente dovuto al guadagno intrinseco M di fotorivelazione. Per questo motivo i rivelatori APD sono maggiormente impiegati nei casi di debole potenza ottica rivelata ed il ricevitore si trova a lavorare in regime limitato dal rumore termico.
Nel regime dominato dal rumore shot, invece, si ha

che evidenzia una perdita pari al fattore di rumorosità in eccesso F dello APD rispetto al diodo p-i-n. Nei casi in cui il ricevitore si trova a lavorare in un caso intermedio si deve valutare di volta in volta l'opportunità, data una certa struttura di ricevitore e, quindi, dato un certo valore della 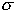 2Tot, di usare un APD o un p-i-n. A questo scopo riscriviamo in modo sintetico il rapporto segnale-rumore per il caso generale del ricevitore con APD 2Tot, di usare un APD o un p-i-n. A questo scopo riscriviamo in modo sintetico il rapporto segnale-rumore per il caso generale del ricevitore con APD
 , ,
con ovvio significato dei simboli. Si osserva che all'aumentare di M tende a diminuire l'influenza del rumore termico; d'altronde all'aumentare di M tende a crescere anche il fattore di rumore in eccesso F, facendo così aumentare il contributo di rumore shot e di corrente di buio. È naturale pensare che esisterà in ogni condizione un valore ottimo di M che massimizza il rapporto segnale-rumore. Sostituendo nella relazione precedente l'espressione di F ed uguagliando a zero la derivata rispetto ad M, si ottiene un'equazione per calcolare il valore ottimo Mopt
 . .
Si noti che Mopt risulta indipendente dalla banda del ricevitore. Nella figura seguente è riportato l'andamento di Mopt al variare di P0 e per vari valori di k, in cui sono stati adottati i parametri RL = 1 K , FA = 3 dB, R = 1 A/W, Id = 2 nA, T = 290 °K. , FA = 3 dB, R = 1 A/W, Id = 2 nA, T = 290 °K.

Fig. 3.11 - Guadagno ottimo dello APD in funzione di P0.
Quando il guadagno è forte e k > 10 -2, si può trascurare il secondo termine nella relazione precedente e si ottiene

la quale mostra l'inversa dipendenza di Mopt da P0 e da k.
3.4.4 - Sensibilità di un Ricevitore
Si definisce sensibilità (sensitivity) del ricevitore quel valore minimo di potenza  che consente di ottenere un prefissato valore del rapporto segnale rumore che consente di ottenere un prefissato valore del rapporto segnale rumore  per una data applicazione. Sostituendo I = R* per una data applicazione. Sostituendo I = R* nell'espressione dello SNRAPD e ricavando nell'espressione dello SNRAPD e ricavando  si ottiene si ottiene
 . .
Dalla precedente relazione si ottiene immediatamente, in condizioni di regime limitato dal rumore di fotorivelazione (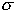 2D = 2D = 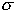 2Tot = 0), che 2Tot = 0), che

mentre, nel caso di regime limitato dal rumore termico ([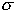 2Tot/M2] >> 2qFR 2Tot/M2] >> 2qFR B), si ottiene B), si ottiene
 . .
Sebbene nell'analisi precedente ci si è riferiti ad un ricevitore con APD, si possono ricavare risultati validi anche per un ricevitore con diodo p-i-n semplicemente ponendo F = M = 1.
|
 .
.








 .
.
 ,
,
 ,
, .
.
 .
.



 .
.
 .
. .
.
 .
. .
.
 .
. .
.
 .
.


 ,
, .
.

 .
.