Lista esercitazioni Metodi ASB anno 2009/2010 

1)

Considerare la sequenza ottenuta campionado la funzione s1(t)=exp(j*2*pi*t/T0) con T0=1 s, e dt=0.01. Fare il grafico sul piano di Gauss, parte reale-parte immaginaria della sequenza.

Evidenziare con due circoletti di diverso colore i punti s(0) e s(dt).

Fare i grafici rispetto al tempo della parte reale e della parte immaginaria di s1(t).


Ripetere le operazioni precedenti per s-1(t)=exp(-j*2*pi*t/T0).

Fare il grafico rispetto al tempo del segnale s(t)=s-1(t)+s1(t)

2)
Considerati i coefficienti complessi S1=5ej*pi/4 e S-1=5e-j*pi/4 si ripetano i punti descritti nell'esercizio 1)  per i segnali   s1(t)=S1exp(j*2*pi*t/T0), s-1(t)=S-1exp(-j*2*pi*t/T0) e s(t)=s-1(t)+s1(t).

3)
Dato lo sviluppo in serie di Fourier di un'onda quadra con periodo T0=2 s, 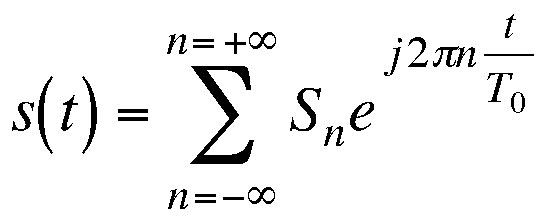 caratterizzato dai seguenti valori dei coefficienti.
S0=0.5 e Sn=0.5*(sin(n*pi/2)/(n*pi/2)) per n≠0.
Fare il grafico rispetto al tempo delle componenti s|n|(t)=s-n(t)+s+n(t) per n=0, 1,2,...,9. In pratica si avranno 9 grafici dove saranno visualizzate le componenti per n=0, n=1, n=2 etc.
(N.B. in realtà i coefficienti per n pari sono nulli quindi la somma riguarderà solo n=0,1,3,5,7,9)

Sovrapporre a tali grafici il grafico della onda quadra ottenuta tramite il comando square(.) di matlab. es. onda_q=0.5+0.5*square(2*pi*(1/T0)*t)

Considerare poi i segnali ottenuti in modo incrementale le varie componenti: primo passo -> grafico di  s0(t)+s|1|(t), secondo passo ->grafico di  s0(t)+s|1|(t)+s|2|(t) etc.

Per valutare il contributo delle componenti a frequenza maggiore fare il grafico della somma delle componenti dalla 5 alla 9, s|5|(t)+s|7|(t)+s|9|(t)

In ogni grafico confrontare con l'onda quadra completa.


4)

Date la sequenza periodica ottenuta campionando con tempo di campionamento T=1 s,  il  segnale tempo continuo x1(t)=cos(2*p*t/8), utilizzare l'algoritmo di fft per calcolarne la TDF. Tracciare i grafici modulo e fase della TDF. Curare la determinazione del corretto periodo delle sequenze campionate e la corretta taratura dell'asse frequenziale. In particolare eseguire i grafici con e senza l'utilizzo del comando  fftshift( ) che serve per centrare attorno ad f = 0 i valori stimati della TDF.

Utilizzare il comando ifft( ) per realizzare la trasformata di Fourier inversa e farne il grafico confrontando il risultato con la sequenza di partenza.

vedere dispensa

 

5)

 

Calcolare la TDF del treno di impulsi dato dalla ripetizione periodica della sequenza x[n]=[1 1 1 1 0 0 0 0 ]. Tracciare i grafici modulo e fase della TDF. Curare la corretta taratura dell'asse frequenziale.

In particolare eseguire i grafici con e senza l'utilizzo del comando  fftshift( ) che serve per centrare attorno ad f = 0 i valori stimati della TDF.

Utilizzare il comando ifft( ) per realizzare la trasformata di Fourier inversa e farne il grafico confrontando il risultato con la sequenza di partenza.

vedere dispensa