Esercitazione 18/5/2009

Caricare il vettore hemo contenuto nel file hemo_1s.mat.

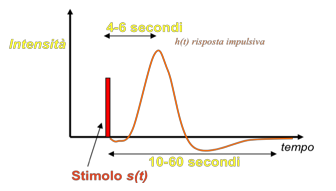
Questo vettore rappresenta la risposta emodinamica ad uno stimolo breve, cos“ come viene misurata dalla risonanza magnetica per immagini a livello cerebrale (Risonanza magnetica per immagini, fMRI). Questo stimolo pu˜ considerarsi di tipo impulsivo.

La particolare risposta emodinamica in hemo_1s.mat  descritta con un dt=1s.

Di seguito  riportata la risposta ad un impulso

risposta a due impulsi

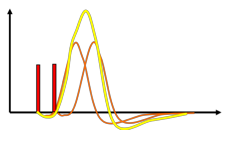
In generale se h(t)  la risposta impulsiva, vista la linearitˆ e la tempo invarianza del sistema, la risposta alla somma di impulsi ritardati si considera come la somma delle risposte ritardate.

1) Dato un vettore con dt=1s, che descrive l'andamento dello stimolo fornito ad un soggetto, calcolare la risposta attesa, misurata tramite fMRI usando la convoluzione tra lo stimolo e la risposta emodinamica in hemo_1s.mat.

a) uno stimolo al tempo t=5 s

b) due stimoli ai tempi t=5s e t=25s

c)due stimoli a t=5s e t=8s

d) caricare la descrizione degli stimoli nella serie paradigma.mat, farne il grafico e calcolarne la risposta del sistema detta y, convoluzione tra hemo e il paradigma stesso.

2) Considerare il caso d).

a)Fare il grafico della risposta in frequenza del sistema utilizzando la trasformata discreta di Fourier di hemo.

b) Fare il grafico della trasformata del paradigma e della y.

c) Calcolare la convoluzione tra il paradigma e hemo utilizzando la TDF.

5) Caricare la risposta emodinamica rappresentata con un dt=2 s e contenuta nel file hemo_2s.mat. Considerare la descrizione del paradigma in paradigma_2_V6.mat. Ottenere la convoluzione tra la risposta emodinamica e il paradigma.

Usare la risposta ottenuta come regressore nell'analisi delle serie temporali serie_37_36_V6.mat, serie_37_37_V6.mat e serie_42_30_V6.mat (per fare ci˜ occorrerˆ prendere solo i primi 100 campioni della serie ottenuta dalla convoluzione, in modo da avere gli stessi punti temporali delle serie in oggetto).