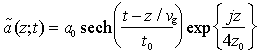Riprendiamo in esame in questo capitolo alcuni dei fenomeni visti, in chiave negativa, nei capitoli precedenti per vedere come sia possibile sfruttarli a favore della trasmissione di segnali ottici su fibra. In particolare vedremo come si stia sviluppando una nuova tecnologia di trasmissione basata sui fenomeni dispersivi nonlineari, relativi alle fibre monomodali, esaminati nel dettaglio in precedenza. L'attenzione è stata rivolta alle fibre monomodali perchè, come si ricorderà, è tale tipo di fibra che potenzialemente può garantire una maggiore distanza di trasmissione senza necessità di un ripetitore di segnale.
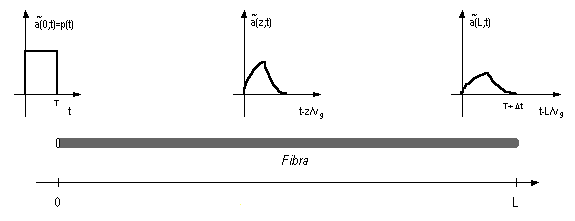
Rammentiamo che uno dei fenomeni che limitano la trasmissione ad alta velocità su lunghe tratte di fibra è la dispersione intramodale (Cap. 1.3) sperimentata dal segnale in una fibra monomodo per effetto della dispersione del materiale e di guida d'onda. L'effetto di tale fenomeno sull'impulso passa-banda alla frequenza f0, corrispondente alla trasmissione di un simbolo pari ad "1" in un sistema IM/DD, è quello di provocare un progressivo "allargamento" dell'inviluppo dell'impulso stesso man mano che il segnale si propaga in fibra, come è suggerito dalla figura seguente.
Possibili contromisure alla dispersione intramodale, che può essere vista come un fenomeno di distorsione lineare, consistono in un certo ammontare di filtraggio sagomatore in ricezione con l'intento di "equalizzare" la risposta della fibra. Nei ricevitori per sistemi ad alta velocità non è, però, possibile allo stato attuale dell'arte realizzare raffinati equalizzatori (come quelli presenti nei sistemi radio) che richiederebbero componenti a banda larghissima non facilmente progettabili. Quando la dispersione diventa notevole e la velocità di trasmissione è alta, l'equalizzazione in ricezione si rivela impraticabile 18.
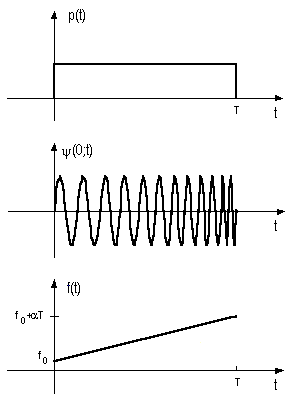
ove p(t) è l'impulso di trasmissione lentamente variabile nei confronti di 1/f0 diverso da zero sull'intervallo [0, T) ed associato al simbolo "1" (figura seguente). La frequenza istantanea di oscillazione di tale segnale è f(t) = f0 +
In questo modo il fronte di discesa "si propaga più velocemente" del fronte di salita, tendendo a raggiungerlo e compensando l'allargamento dovuto alla dispersione cromatica. Esiste una lunghezza ottima di propagazione per cui l'impulso ha durata minima; al di là di questa lunghezza il fronte di salita "sopravanza" quello di discesa e l'impulso ricomincia ad allargarsi per l'effetto congiunto di dispersione e chirp (adesso controproducente).
Prima di studiare ulteriormente la possibilità di realizzare "automaticamente" la compensazione della dispersione inducendo un chirp sul segnale trasmesso attraverso l'effetto Kerr, ci proponiamo di ricavare l'equazione di propagazione del mezzo dispersivo la cui risposta in frequenza è stata ricavata nel Cap. 1 19. Consideriamo, dunque, di nuovo la relazione
che lega la trasformata di Fourier
Derivando rispetto a z entrambi i membri si ha immediatamente una equazione differenziale del primo ordine per
Antitrasformando questa relazione per tornare in ambito temporale, otteniamo una equazione differenziale alle derivate parziali che regola la propagazione del pacchetto d'onda nel mezzo omogeneo, isotropo, lineare, senza perdite e dispersivo
che, in assenza di dispersione (D = 0), si riduce alla familiare equazione differenziale per la propagazione di un'onda progressiva.
Il secondo termine a II membro nell'equazione di propagazione precedente è, dunque, responsabile dell'allargamento per dispersione di un impulso lanciato in fibra. Nel precedente paragrafo si è analizzata la possibilità di compensare questo termine attraverso un opportuno "chirping" dell'impulso. Un modo per ottenere "automaticamente" il chirping necessario alla compensazione della dispersione è quello di aumentare l'ampiezza dell'impulso lanciato in fibra in modo che l'automodulazione di fase dovuta all'effetto Kerr (che è stata discussa nel Cap. 1) provochi lo stesso effetto di compressione dell'impulso. Ricordiamo che per effetto Kerr l'indice di rifrazione del mezzo risulta dipendente dall'ampiezza del campo elettrico presente in fibra secondo la relazione
ove n(f0) è l'indice di rifrazione in regime lineare alla frequenza di centro banda, n' è il corrispondente valore aumentato per effetto Kerr, P è la potenza del segnale in fibra, A è l'area della sezione trasversale del nucleo della fibra ed
ove, questa volta, n2 è un diverso coefficiente Kerr proporzionale ad
ove, come già detto, il termine di sfasamento è dovuto alla sola componente nonlineare della dispersione. La variazione spaziale
per cui il termine di gradiente spaziale addizionale da aggiungere a secondo membro dell'equazione di propagazione è pari a
L'equazione di propagazione del pacchetto d'onda inclusiva dell'effetto di automodulazione di fase è dunque
ovvero
Può accadere che la dispersione nonlineare indotta dall'effetto Kerr compensi perfettamente la dispersione lineare del mezzo. Quando ciò si verifica, la soluzione della precedente si dice onda solitaria e si propaga nel mezzo senza distorsioni. Esistono, poi, onde solitarie che godono di una particolare proprietà di ortogonalità: quando due di queste soluzioni vengono ad "interagire", come nel caso di due impulsi contropropaganti sulla stessa fibra che si trovano a "collidere", esse non si influenzano reciprocamente bensì mantengono la propria "individualità" dopo l'interazione, cioè conservano la stessa forma dell'inviluppo (proprietà non ovvia in regime di propagazione nonlineare). Per questo motivo tali soluzioni dell'equazione d'onda si dicono solitoni.
che provoca uno scostamento nella frequenza istantanea del pacchetto d'onda dal valore f0 relativo al caso di propagazione lineare pari a
Poiché n2 > 0, sul fronte di salita dell'impulso (derivata temporale dell'inviluppo positiva) la frequenza è minore di f0, mentre sul fronte di discesa la frequenza è maggiore. Affinché questo impulso "chirp" si propaghi senza allargamento, le frequenze più alte (relative al fronte di discesa) devono propagarsi più velocemente delle frequenze più basse relative al fronte di salita. La velocità di gruppo deve essere crescente con la frequenza e, quindi, il coefficiente di dispersione D deve risultare positivo: la compensazione è possible solo in condizioni di propagazione anomala (
L'equazione di propagazione viene usualmente scritta usando tempi, distanze ed ampiezze opportunamente normalizzate. Sia t0 un parametro di durata dell'impulso p(t) lanciato in fibra; si adotta, allora, come coordinata temporale la seguente coordinata normalizzata che "si propaga solidalmente con l'onda"
La coordinata spaziale viene, poi, normalizzata rispetto alla distanza 2z0 = 2
ed infine le ampiezze del pacchetto d'onda sono scalate della quantità a0
Se l'ampiezza dell'impulso lanciato in fibra è molto più piccola di a0, la dispersione lineare tende a dominare; se invece |
che è la cosiddetta equazione di Schrödinger nonlineare. Per ricavare una soluzione in forma di solitone di questa equazione, si cerca un andamento di
con la condizione V(0) = 1 derivante dalla normalizzazione e
Affinchè effettivamente l'inviluppo V(
e, quindi, sostituendo nella precedente,
Motliplicando entrambi i membri per dV(
con C costante opportuna. Imponendo le condizioni al contorno viste, si trova immediatamente C = 0. Inoltre, aggiungendo le condizioni "iniziali", si ha K = 1/2, per cui la precedente diventa
ovvero, dividendo per V(
Questa equazione elementare ha come soluzione particolare con V(0) = 1 la seguente
Unendo le relazioni ottenute si ha infine
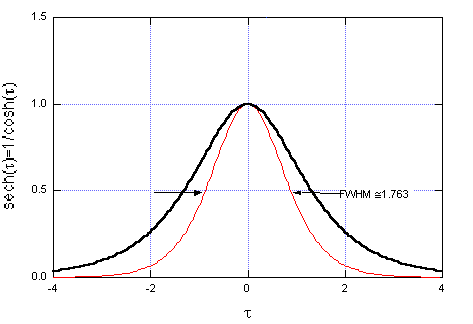
ove sech(
Denormalizzando la soluzione si ottiene
che indica chiaramente come l'impulso del tipo sech(°) si propaghi senza distorsione ed in particolare senza allargamento, realizzando così la compensazione della dispersione lineare attraverso la SPM.
La quantità t0 rappresenta una misura della durata del solitone e può considerarsi una variabile indipendente, nel senso che si possono, in teoria, realizzare solitoni con durate arbitrarie. In realtà alla durata del solitone è legata l'ampiezza massima a0 del medesimo, che deve aumentare al diminuire della durata stessa. La possibilità di ottenere solitoni in fibra è stata prevista teoricamente nel 1973 attraverso la derivazione dell'equazione di Schrödinger per la propagazione del pacchetto d'onda in fibra, mentre l'osservazione sperimentale della formazione di un solitone si è avuta nel 1980. In questo esperimento è stato usato un laser a gas pompato da un laser Nd:YAG (Niodimio:Ittrio Alluminio Granato) con impulsi della durata di 7 ps per una ampiezza massima, calcolata secondo i parametri della fibra, in 1.2 W.
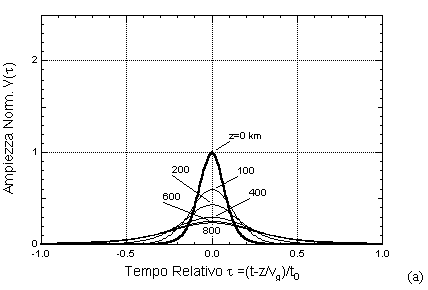
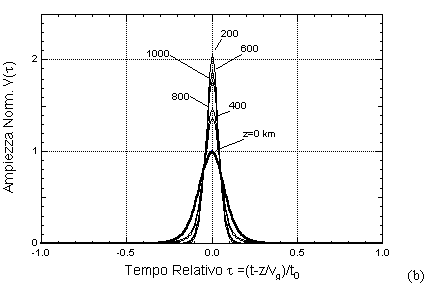
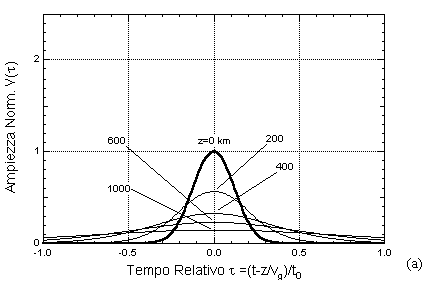
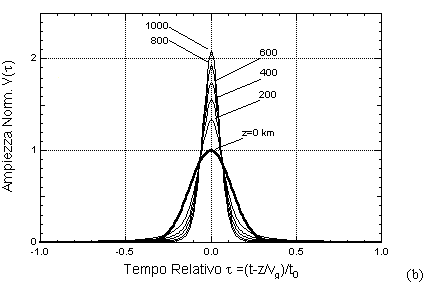
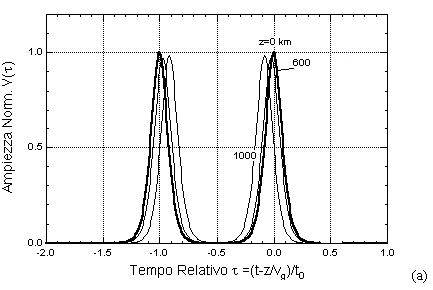
il solitone non si forma e l'impulso viene rapidamente disperso, come mostrato nella figura (a) seguente; se l'ampiezza è superiore, il solitone viene ad eccitarsi man mano che l'impulso si propaga in fibra, mentre la parte dell'energia dell'impulso eccedente viene dissipata in code secondarie che rapidamente si disperdono, come nell'esempio della figura (b) seguente.
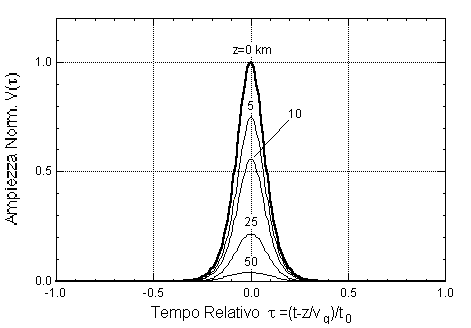
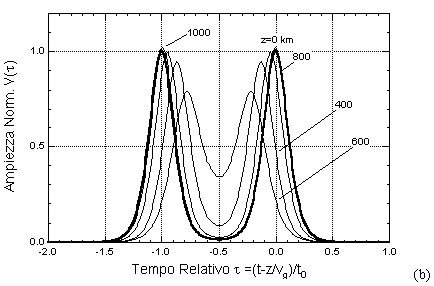
Il solitone possiede anche una proprietà di "robustezza", nel senso che non è necessario che l'impulso generato dal LASER di trasmissione abbia esattamente la forma prescritta di sech(°); ogni "ragionevole" forma d'onda (Gaussiana o similare) tende ad evolvere verso il solitone, purchè l'ampiezza della medesima sia adeguatamente maggiore della a0 prevista per la soluzione dell'equazione di Schrödinger. La figura (a) seguente mostra l'evoluzione di un impulso Gaussiano con una potenza di picco pari a +10 dBm sufficiente ad innescare la propagazione solitonica, mentre la (b) è relativa al caso di potenza di picco 0 dBm, in cui il solitone non può formarsi e l'impulso si allarga perchè la dispersione lineare è dominante.
C'è da osservare che la relazione
è stata ricavata nell'ipotesi di mezzo senza perdite. In realtà lanciando un solitone in fibra si deve tener conto che la potenza ottica dell'impulso decresce man mano che questo si propaga. È chiaro, dunque, che il solitone cessa di essere tale non appena l'ampiezza dell'inviluppo, per effetto dell'attenuazione della fibra, non è più tale da poter provocare una compensazione della dispersione lineare attraverso l'effetto Kerr.
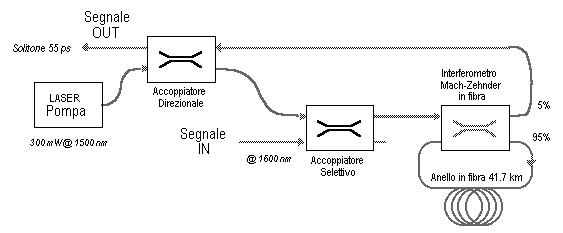
In questo modo, sono stati condotti molti esperimenti di trasmissione su anelli di fibra con amplificazione ripetuta; di seguito è mostrata la disposizione di uno dei primi di questi esperimenti, che prevedeva amplificazione Raman con pompa a 1.46
Tali esperimenti hanno consentito di rivelare solitoni trasmessi su di una lunghezza di diverse migliaia di Km di fibra. Recentemente è stata anche dimostrata la possibilità di usare amplificazioni ripetute di solitoni mediante EDFA per compensare le perdite delle varie tratte in fibra. Con la tecnica dell'anello di fibra (75 Km con 3 EDFA) si è arrivati alla trasmissione di solitoni da 50 ps su di una distanza di 10.000 Km.
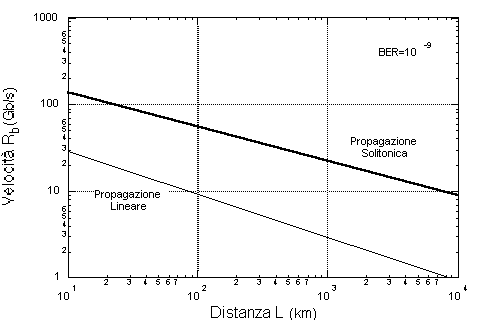
La figura seguente mostra, infine, il confronto tra la capacità di trasmissione di un sistema IM/DD con impulsi Gaussiani a 1.5
|
.gif)
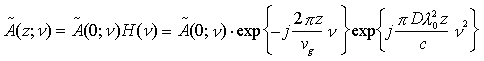 .
.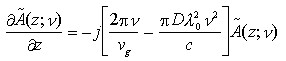 .
.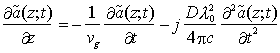
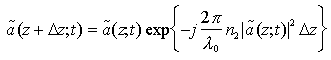
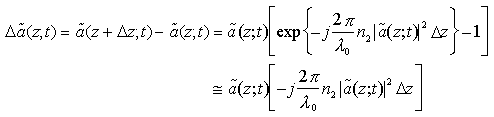
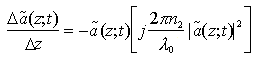 .
.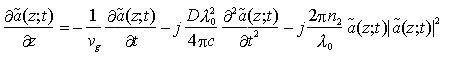
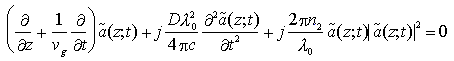 .
.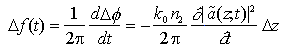 .
.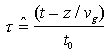 .
.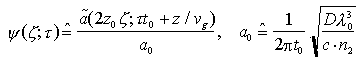 .
.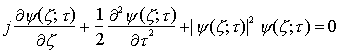
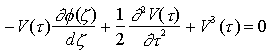 .
.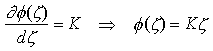
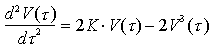 .
.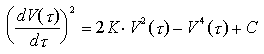
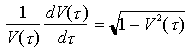
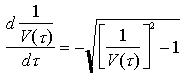 .
.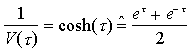 .
.